![[pi]](pi.gif) radians in a
complete revolution or circle.
It is important to differentiate between an angle (a set of points) and
its measure denoted m
radians in a
complete revolution or circle.
It is important to differentiate between an angle (a set of points) and
its measure denoted mAnother study of angles involves eclipses and transits. The student is assumed to be familiar with such events, especially, the pair of venus transits in June 2004 and 2012. These are rare enough that no one alive has seen one.
| An angle is the union of two rays with the same endpoint. |
The rays forming an angle are its sides.
The vertex is the common endpoint of the two rays.
The symbol for angle (![]() ) can easily be confused with the symbol
for less than (<).
One important classification of angles is based on their angle measure.
Angles are usually measured in either degrees or radians.
(See also an introduction in Numbers Lesson 11.)
Occasionally we see references to grade (1 grade=0.9°).
Although some (our text) omit the degree symbol, we don't expect you ever to.
There are 360° or 2
) can easily be confused with the symbol
for less than (<).
One important classification of angles is based on their angle measure.
Angles are usually measured in either degrees or radians.
(See also an introduction in Numbers Lesson 11.)
Occasionally we see references to grade (1 grade=0.9°).
Although some (our text) omit the degree symbol, we don't expect you ever to.
There are 360° or 2![[pi]](pi.gif) radians in a
complete revolution or circle.
It is important to differentiate between an angle (a set of points) and
its measure denoted m
radians in a
complete revolution or circle.
It is important to differentiate between an angle (a set of points) and
its measure denoted m![]() .
A zero angle is where the two rays share the same points and
coincide. They thus appear to be a single ray.
It is so named because of its zero angle measure.
An acute angle is one whose measure is strictly between zero and 90°.
A right angle is one whose measure is exactly 90°.
On a drawing the symbol
.
A zero angle is where the two rays share the same points and
coincide. They thus appear to be a single ray.
It is so named because of its zero angle measure.
An acute angle is one whose measure is strictly between zero and 90°.
A right angle is one whose measure is exactly 90°.
On a drawing the symbol ![]() can be used to label two rays or segments as perpendicular (at right angles).
In symbols we write that one line or segment is perpendicular to another using
the symbol
can be used to label two rays or segments as perpendicular (at right angles).
In symbols we write that one line or segment is perpendicular to another using
the symbol ![]() .
An obtuse angle is one whose measure is strictly between 90° and 180°.
A straight angle is one in which both rays are opposite and
form a [straight] line. Its measure is 180°.
Not all geometries accept zero and straight angles as angles, often
specifying that the component rays must be nonidentical and nonopposite.
Two more angle terms are
reflex angle
for angles between 180° and 360° and
full angle
or 360° (one revolution).
Angles can sometimes be named by their vertex alone
(
.
An obtuse angle is one whose measure is strictly between 90° and 180°.
A straight angle is one in which both rays are opposite and
form a [straight] line. Its measure is 180°.
Not all geometries accept zero and straight angles as angles, often
specifying that the component rays must be nonidentical and nonopposite.
Two more angle terms are
reflex angle
for angles between 180° and 360° and
full angle
or 360° (one revolution).
Angles can sometimes be named by their vertex alone
(![]() A),
but since more than one angle often share a vertex this "nickname"
can be ambiguous and a full specification using three points
(
A),
but since more than one angle often share a vertex this "nickname"
can be ambiguous and a full specification using three points
(![]() BAC) is thus necessary.
At other times angles may be designated via a number (see below).
BAC) is thus necessary.
At other times angles may be designated via a number (see below).
| Vertical angles are equal. |

Two lines cut by a transversal are parallel if and only if:
|
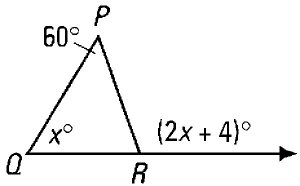 The angle between two sides of a polygon is an interior angle,
whereas the angle formed by one side and extending the other side
of an angle in a polygon is an exterior angle.
They form a linear pair.
Examples of interior angles would be those labelled x and 60º
in the figure left. The angle labelled (2x+4)º
is an exterior angle.
We can also differentiate between the interior and exterior of a polygon
by noting that your right side is toward the interior as you travel
clockwise around a closed figure or on your left side as you travel
counter-clockwise or anti-clockwise as they say on the
other side of the "pond."
The angle between two sides of a polygon is an interior angle,
whereas the angle formed by one side and extending the other side
of an angle in a polygon is an exterior angle.
They form a linear pair.
Examples of interior angles would be those labelled x and 60º
in the figure left. The angle labelled (2x+4)º
is an exterior angle.
We can also differentiate between the interior and exterior of a polygon
by noting that your right side is toward the interior as you travel
clockwise around a closed figure or on your left side as you travel
counter-clockwise or anti-clockwise as they say on the
other side of the "pond."
![[pi]](pi.gif) radians.
Angles inside circles are either central angles if their vertex
is the center of the circle, or inscribed angles if their vertex
is on the circle. (We assume each side includes a point on the circle other
than the vertex.)
A central angle intercepts a portion of the circumference of the circle
termed an arc.
An arc is a minor arc if its central angle is less than 180°.
An arc is a major arc if its central angle is more than 180°.
If an arc is exactly 180° it is termed a semicircle.
Minor arcs are specified using two points (letters) under a curved line,
whereas semicircles and major arcs are specified using three points.
There is the following relationship between a central
angle and its corresponding inscribed angle.
radians.
Angles inside circles are either central angles if their vertex
is the center of the circle, or inscribed angles if their vertex
is on the circle. (We assume each side includes a point on the circle other
than the vertex.)
A central angle intercepts a portion of the circumference of the circle
termed an arc.
An arc is a minor arc if its central angle is less than 180°.
An arc is a major arc if its central angle is more than 180°.
If an arc is exactly 180° it is termed a semicircle.
Minor arcs are specified using two points (letters) under a curved line,
whereas semicircles and major arcs are specified using three points.
There is the following relationship between a central
angle and its corresponding inscribed angle.
| An inscribed angle is half the measure of the central angle intercepting the same arc. |
If you know the measure of a central angle, you can also calculate its arc length as the proportion between this measure over 360° equal to this unknown arc length over the circumference.
The following items can be assumed from figures:
|
The following items cannot be assumed from figures:
|
| Always remember: Geometric diagrams are not drawn to scale. |
| Postulates of Equalities, Inequality, and Operations: | Example: |
|---|---|
| Reflexive | x = x. |
| Symmetric | If x = y, then y = x. |
| Transitive | If x = y and y = z, then x = z. |
| Addition Property of Equality | If x = y, then x + z = y + z. |
| Multiplication Property of Equality | If x = y, then x × z = y × z. |
| Equality to Inequality Property | If x and y are >0 and x+y=z, then z>x and z>y. |
| Substitution Property | If x = y, then x may be substituted for y anywhere. |
An easy way to differentiate among reflexive, symmetric, and the transitive
property is to relate the alphabetic sequence RST with the numeric
sequence 123 and note the number of variables used in each definition.
Subtraction was defined via additive inverses
and division was likewise defined via multiplicative inverses
(Numbers Lesson 2).
Hence the Addition and Multiplication properties above allow those
operations as well.
Also, similar properties for inequalities (< and > but not
![]() )
for the Transitive, Addition,
and Multiplication (for z>0) postulates above hold as well.
The next to last property given above is very similar to the
Triangle Inequality.
Mastering algebra is an underlying theme of geometry,
as are building vocabulary, developing important concepts,
and sharpening critical thinking.
Graphing lines and inequalities on the coordinate plane,
finding slope, determining parallelism or perpendicular,
are a major venue for developing this mathematical prowess.
)
for the Transitive, Addition,
and Multiplication (for z>0) postulates above hold as well.
The next to last property given above is very similar to the
Triangle Inequality.
Mastering algebra is an underlying theme of geometry,
as are building vocabulary, developing important concepts,
and sharpening critical thinking.
Graphing lines and inequalities on the coordinate plane,
finding slope, determining parallelism or perpendicular,
are a major venue for developing this mathematical prowess.
|
If two lines are parallel, then their slopes are equal. If two lines are perpendicular, then the product of their slopes is -1. |
Numbers whose product are -1 are termed negative reciprocals. If the slope of one line is -x and the slope of another is 1/x, then -x • 1/x = -1. Perpendicular lines, of course, always form 90° angles. Other terms for perpendicular are: orthogonal, normal, and, of course, right.
The transitivity property may be used to show two lines parallel to a third line are parallel to each other. This is often termed the Transitivity of Parallelism Theorem. If two lines are perpendicular to the same line, then the two lines are parallel to each other, if they are coplanar. If a line is perpendicular to a line that is parallel to another, then the first line is perpendicular to the other two, again if they are all coplanar. The Euclidean or Plane Geometry we are studying will make this basic assumption.
Proof arguments can be written in many styles, just like there are many different styles of writing: essay, lists of concepts, etc. The two most common forms of proof are two column and paragraph. Examples of each have occurred already: compare the paragraph proof used in Numbers Lesson 3 to show that the primes form an infinite set with the two column proof used in Numbers Lesson 12 to derive the quadratic formula. Traditionally (since 1900) Geometry has used the two column proof with the left column containing the statement and the right column containing the corresponding justification. It is something you must become familiar with. Proofs can also be direct or indirect as described in Numbers Lesson 5. They can also be based on inductive or deductive reasoning as well.
The following basic construction algorithms must be mastered. More will be added later.
If the segment is placed against the edge of the paper, then only one point at a time can be determined by any given radius. You thus must reset the compass radius to find a second point on the same side of the line.
![]() To construct an equilateral triangle draw a line segment
and mark off the desired length.
Set the compass to that length then draw an arc from each end of
the given segment so that they intersect at a point on one side.
(Again, if in doubt complete circles can be used.)
Draw segments connecting each endpoint to the intersection of these
segments. Clearly all three sides are of equal length, the triangle
is thus equilateral, and since the triangle is isosceles three different ways,
by the base angle congruence theorem
(yet to come) it is also equiangular.
To construct an equilateral triangle draw a line segment
and mark off the desired length.
Set the compass to that length then draw an arc from each end of
the given segment so that they intersect at a point on one side.
(Again, if in doubt complete circles can be used.)
Draw segments connecting each endpoint to the intersection of these
segments. Clearly all three sides are of equal length, the triangle
is thus equilateral, and since the triangle is isosceles three different ways,
by the base angle congruence theorem
(yet to come) it is also equiangular.
There are two major ways to construct a regular hexagon. The first method utilizes a circle with radius of the desired hexagon size length. Pick a point on the circle then mark the distance one radii away with your compass. As you procede around the cicle you will make exactly six equally spaced divisions. Connect these in order to complete your hexagon. The second method makes use of the fact that a regular hexagon can be triangulated into six equilateral triangles. Construct an equilateral triangle as above. Draw a circle centered on one vertex and proceed as above.
To construct an angle bisector set the compass to almost any arbitrary but convenient distance. Place the point of the compass at the angle's vertex. Mark auxillary points on each of the angle's rays with the compass at the same distance from the vertex. From each of these two auxillary points draw another arc in the interior of the angle. (A new distance can be selected for these pair, separate from the distance out the arc, but this optional.) The intersection point formed by the arc from each auxillary point are on the line forming the angle bisector. Connect them and extend the line to complete the construction.
Below/on the next page is a maze from your homework.

For homework 3.7.
| BACK | HOMEWORK | ACTIVITY | CONTINUE |
|---|