u4d1 Functions: Domain, Range, Notation, and Ordered Pairs
Vocab Definitions:
Function: A function is a relationship between an input (x) and a special unique output (y). Set: A set is a collection or grouping of all values in a specific category. Domain: The set of all possible inputs for a given function.
Example \hspace{1cm} (2,3), (7,4), (5,6), (0,0)
\hspace{1cm}
domain = \{0,2,5,7\}
Range: The set of all possible outputs for a given function.
Example \hspace{1cm} (2,3), (7,4), (5,6), (0,0)
\hspace{1cm}
range = \{0,3,4,6\}
Functions as Ordered Pairs
All functions can be written as a collection of ordered pairs. We will use ordered pairs to help us determine if a relationship is in fact a function! Review: Ordered Pairs is a pairing of a single input and a single output.
Ordered \ Pair = (input,output) = (x,y)
Steps to check: Is it a Function??
- Step 1: Does the x repeat?
- No: Congrats! It's a Function!!
- Yes: hmmmm we gotta go checkout step 2
- Step 2: Does the x have a new value for y? (in other words does x cheat?)
- No: Congrats! It's a Function!!
- Yes: NOT a FUNCTION!! can't have x creeping with no side chick
Example 1.) Ordered Pairs as a Function
Given (2,3), (4,3), (6,5) and (0,0) Is it a function? What is the domain and range?- Step 1: Does the x repeat?
- No: Congrats! It's a Function!!
Domain = \{0,2,4,6\}
Range is the set of all outputs or a list of all the y values:
Range = \{0,3,5\}
Notice that we don't repeat the 3 twice. Even though there are two 3's as outputs, the set is just a collection of possible values, so only list each one once.
Example 2.) Ordered Pairs as a Function
Given (2,6), (1,3), (0,0), (2,7) and (9,27) Is it a function? What is the domain and range?- Step 1: Does the x repeat?
- Yes: The input 2 repeats.
- Step 2: Does the x have a new value for y?
- Yes: (2,6) and (2,7) this means 2 is creeping with 6 and 7. This is NOT ALLOWED, so this is NOT a Function.
Domain = \{0,1,2,9\}
Range is the set of all outputs or a list of all the y values:
Range = \{0,3,6,7,27\}
Example 3.) Ordered Pairs as a Function
Given (1,2), (2,4), (0,0), (4,8), (1,2) and (3,6) Is it a function? What is the domain and range?- Step 1: Does the x repeat?
- Yes: The input 1 repeats.
- Step 2: Does the x have a new value for y?
- No: (1,2) and (1,2) this means 1 as an input always has 2 as an output. It is a Function.
Domain = \{0,1,2,3,4\}
Range is the set of all outputs or a list of all the y values:
Range = \{0,2,4,6,8\}
I picked these ordered pairs very carefully because there is a extra special relationship between the inputs and the output. If you look carefully can you see a rule about what is happening to the input to make the output?
2 \cdot input = output
We can write this as an equation using function notation.
f(x)=2 \cdot x
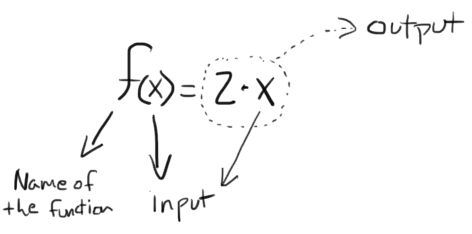
Functions as Equations
Many functions can be written as equations using Function Notation we just learned. For example given:
g(x)=3x+4
We know this is a function named g and its input is any value of x we can think of that gives a reasonable result! This means we can try plugging any values in for x and check and see if the outputs make sense. It's pretty clear that if we started putting colors in for x the result would make no sense. However, If we plug in any numerical value for x we will get a new numerical value as an output!!! So lets try to plug in 4 and 2. In function notation this is done by asking what is:
\\
g(x)=3x+4 \hspace{1cm} g(x)=3x+4 \\
g( \ )=3( \ )+4 \hspace{1cm} g( \ )=3( \ )+4 \\
g(4)=3(4)+4 \hspace{.9cm} g(2)=3(2)+4 \\
g(4)=12 +4 \hspace{1.2cm} g(2)=6+4 \\
g(4)=18 \hspace{2cm} g(2)=10 \\
If we want to write these results as ordered pairs they would be: (4,18) and (2,10)
Example 1.)
Given:
h(x) = -2x-9
find:
h(4) =
This function is named h and has an input of 4. We should set up the problem waiting for 4 to be plugged in, and then solve.
\\
h( \ ) = -2( \ ) -9
\\
h(4) = -2(4) -9
\\
h(4) = -8 -9
\\
h(4) = -17
Written as an ordered pair this result would be: (4,-17)
For Teachers: