Geometry!
Practical geometry
Geometry originated as a practical science concerned with surveying, measurements, areas, and volumes. Formulas like the Pythagorean theorem, circumference and area of a circle, area of a triangle, volume of a cylinder, sphere, and a pyramid were developed to describe common objects. A Greek philosopher named Thales had an idea about similar shapes and scale over 2,600 years ago. The geometric formulas and Thales idea helped early scientists and astronomers make amazing measurements. These ideas were revolutionary. They helped artists, architects, warriors, and many others.
Axiomatic geometry
Euclid, another ancient Greek philosopher took a more abstract approach in his his book “Elements.” Euclid introduced certain axioms, or postulates, (basic ideas that are assumed to be true) expressing self-evident properties of points, lines, and planes (the most basic building blocks for geometry.) He went on to prove more and more complex geometric ideas using rules of logic. This approach to geometry is called “Axiomatic Geometry,” because it is based not on measurements and observations, but on assumptions called axioms.
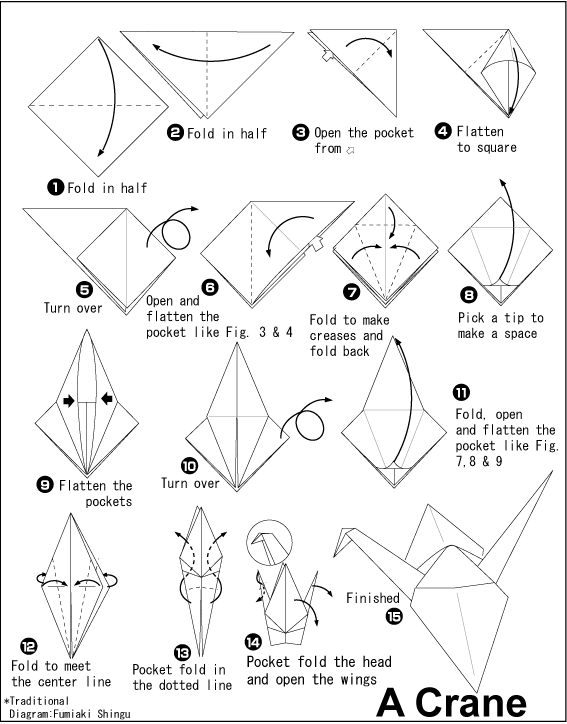
We will study both axiomatic and practical geometry. Some really fun stuff can be done with practical geometry, like oragami! Even games like basketball and football use ideas taken from geometry.
Main Topics:
- Euclidean Geometry
- Measurements, similarity, common shapes, drawing and constructing with paper, straightedge and compass.
- History of Geometry
- Selected achievements from ancient Greece and other cultures.