Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.

He will swallow up death forever. The Sovereign Lord will wipe away the tears from all faces; he will remove his people’s disgrace from all the earth. The Lord has spoken. Isaiah 25:8 NIV

1-03 Linear Equations in Two Variables

Some species of bamboo can grow very quickly. One type can grow 910 mm in a 24 hour period making it the fastest growing plant in the world. The bamboo growth rate is an average of 38 mm/hr. There are many situations that involve a rate of change with time. For example, cars on a highway can travel 60 miles per hour for several hours. These situations are examples of linear relationships.

Linear Functions

A linear function is a function whose graph is a line. Linear functions can be written in the slope-intercept form of a line

y = mx + b

where m is the constant rate of change, or slope, and the y-intercept of the function is (0, b).

Slope

Often knowing the rate of change of something is important such as "What is the rate of change of the water height on the beach as the tide comes in?" or "What is the rate of change of the number of monarch butterflies?" Rate-of-change is how fast something is changing, and it is the slope of a linear function.

Given two points on a line, (x₁, y₁) and (x₂, y₂), the slope, m, is the rise/run.

$$ \text{slope} = \frac{\text{rise}}{\text{run}} $$

$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$

Slope indicates the steepness of a line. The greater the absolute value of the slope, the steeper the line is.

The slope also shows whether the line is rising or falling from left to right.

• If m is positive, the line rises from left to right.
• If m = 0, the line is horizontal.
• If m is negative, the line falls from left to right.
• If m is undefined (divided by zero), the line is vertical.

Parallel lines are two lines in the same plane that do not intersect so that they go in the same direction. Parallel lines have the same slope. Perpendicular lines are two lines that intersect to form a right angle. The slopes of perpendicular lines are negative reciprocals.

Parallel and Perpendicular Lines

Two lines are parallel lines if they do not intersect. The slopes of the lines are the same.

• y = m₁x + b₁ and y = m₂x + b₂ are parallel if m₁ = m₂.

Two lines are perpendicular lines if they intersect at right angles.

• y = m₁x + b₁ and y = m₂x + b₂ are perpendicular if m₁·m₂ = −1, and so \(m_2 = -\frac{1}{m_1}\).

Write the Point-Slope Form of a Linear Equation

After learning the rate-of-change of a situation, sometimes it is important to have a mathematical model for the situation. A linear function through two points can be found using the Point-Slope form of a line. This formula is derived from the slope formula.

$$ m = \frac{y - y_1}{x - x_1} $$

Multiply both sides by x − x₁.

m(x − x₁) = y − y₁

Use the symmetric property to change the order.

y − y₁ = m(x − x₁)

Write an Equation for a Linear Function

It is possible to write a linear function if just two pieces of information are known: the slope and a point the line passes through. Just take those and substitute those into the point-slope form of a line. Then solve for y to put it into slope-intercept form.

Write a Linear Equation from a Graph

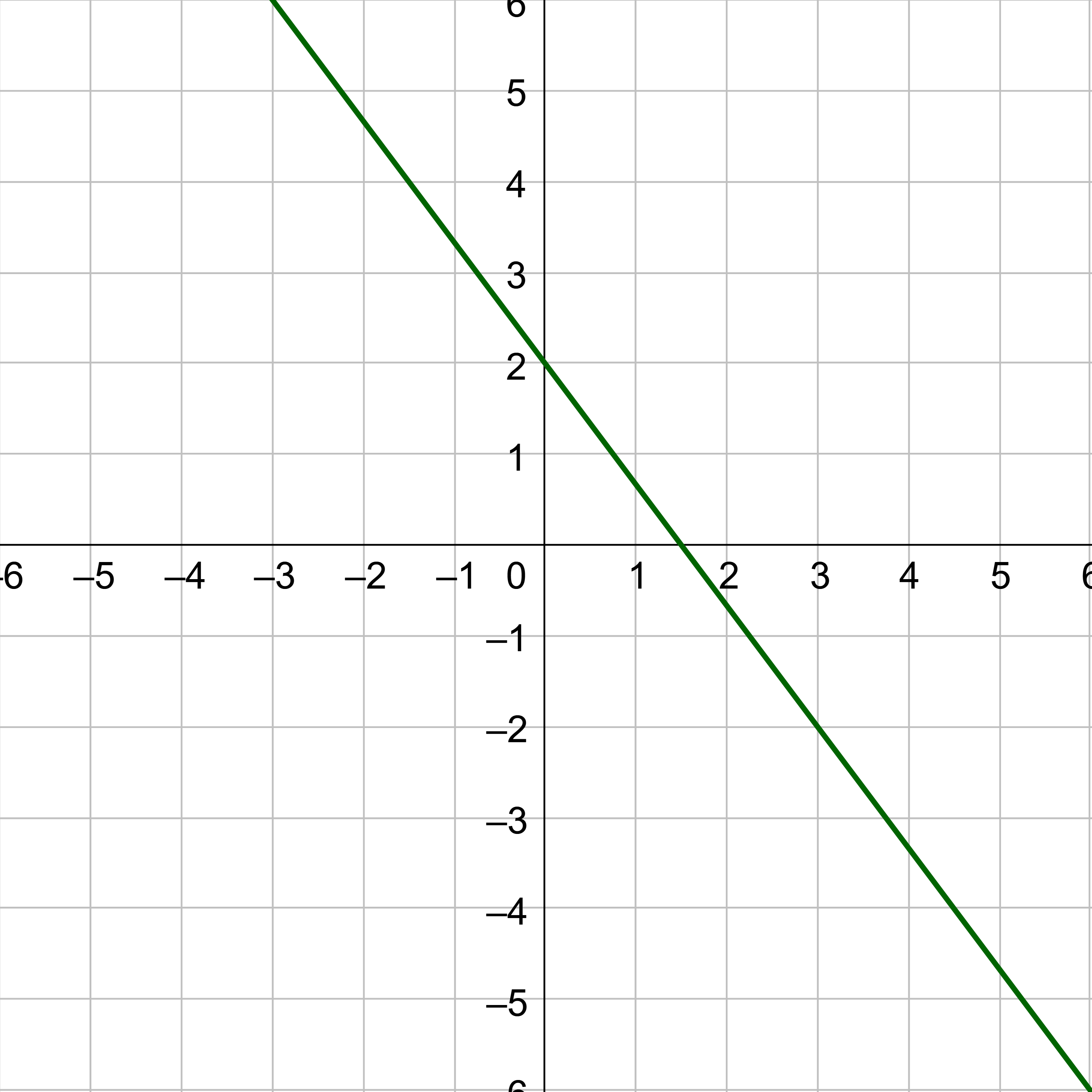
Write the equation of the line in the graph.

Solution

First find the slope. Pick two points on the line such as points A(−1, 1) and B(2, −1). Then use the slope formula to find the slope. You could also just count the rise and run between the points from the graph.

$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$

$$ m = \frac{-1 - 1}{2 - (-1)} $$

$$ m = -\frac{2}{3} $$

Now substitute the slope and one of the points, (2, −1), into the point-slope formula. It does not matter which point you use.

y − y₁ = m(x − x₁)

$$ y - (-1) = -\frac{2}{3}(x - 2) $$

Distribute.

$$ y + 1 = -\frac{2}{3}x + \frac{4}{3} $$

Solve for y.

$$ y = -\frac{2}{3}x + \frac{1}{3} $$

Find a Line Parallel to a Given Line

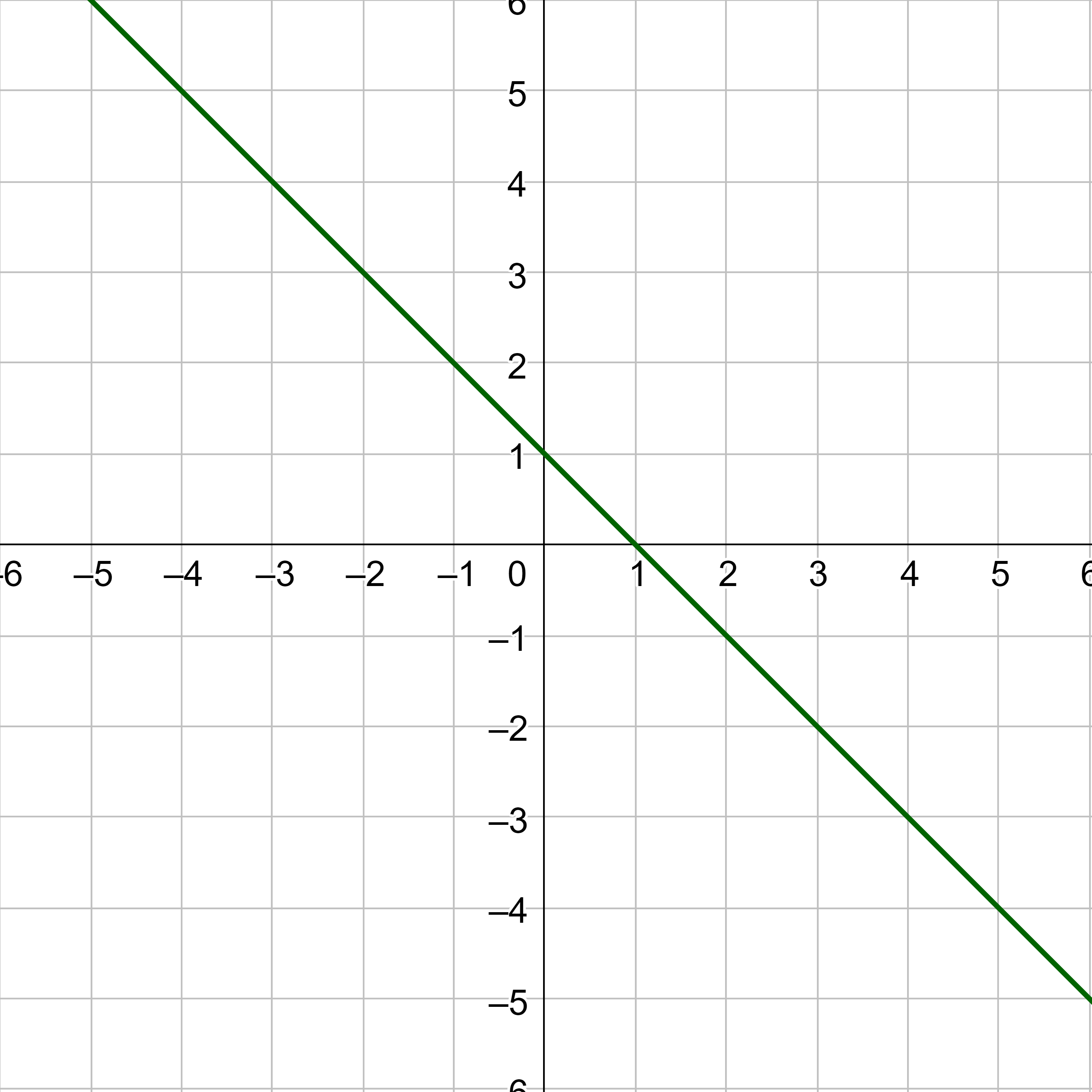
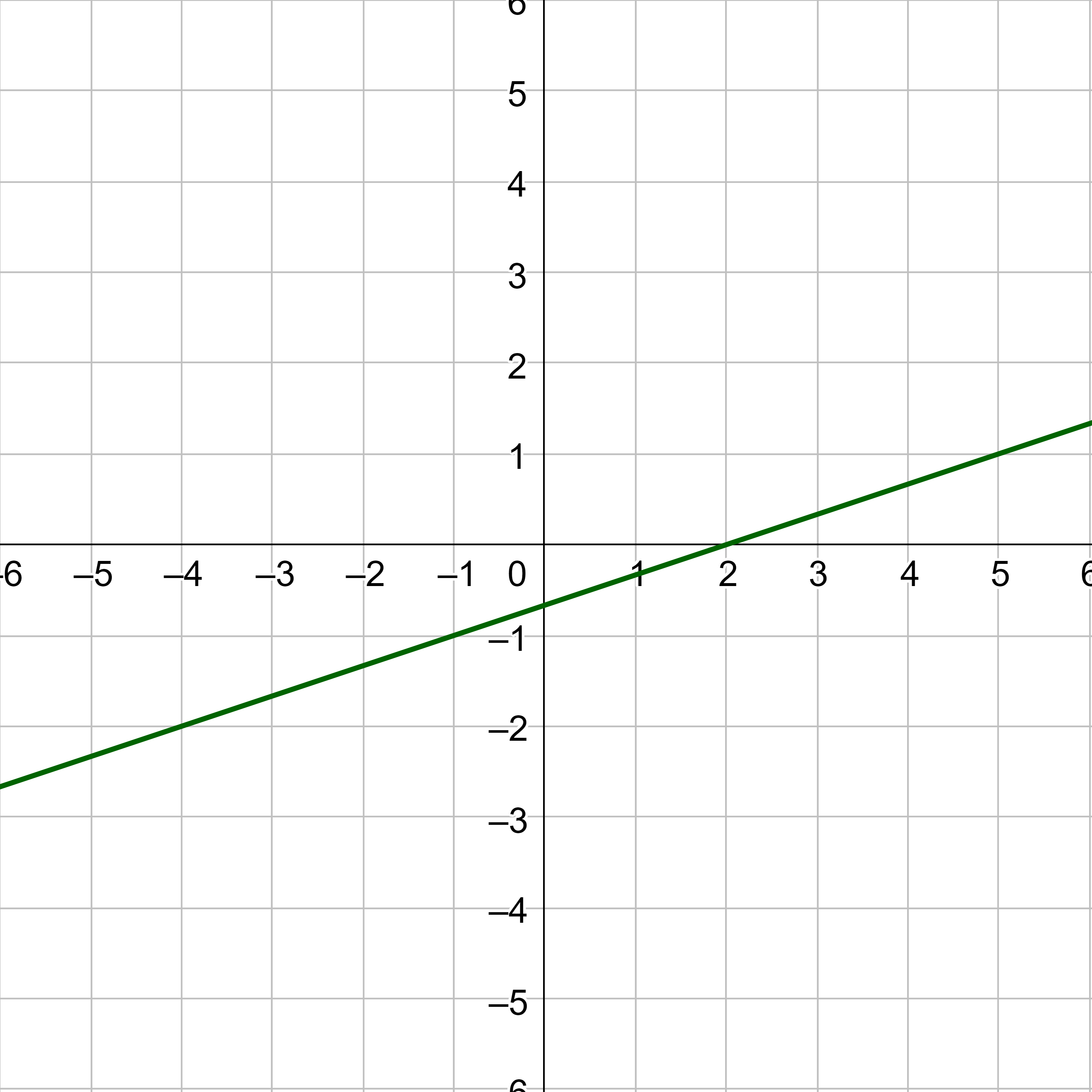
Find the equation of a line parallel to y = −2x + 4 that passes through the point (2, −3).

Solution

First find the slope. The question asks for a line parallel to the given line, and the slopes of parallel lines are the same. The slope of the given line is −2, so the slope of the desired line is also m = −2.

The point (x₁, y₁) is (2, −3). Substitute those into the point-slope form of a line.

y − y₁ = m(x − x₁)

y − (−3) = −2(x − 2)

Distribute.

y + 3 = −2x + 4

Solve for y.

y = −2x + 1

To illustrate that the lines are in fact parallel, figure 7 shows the graphs of both lines.

Find the Equation of a Perpendicular Line

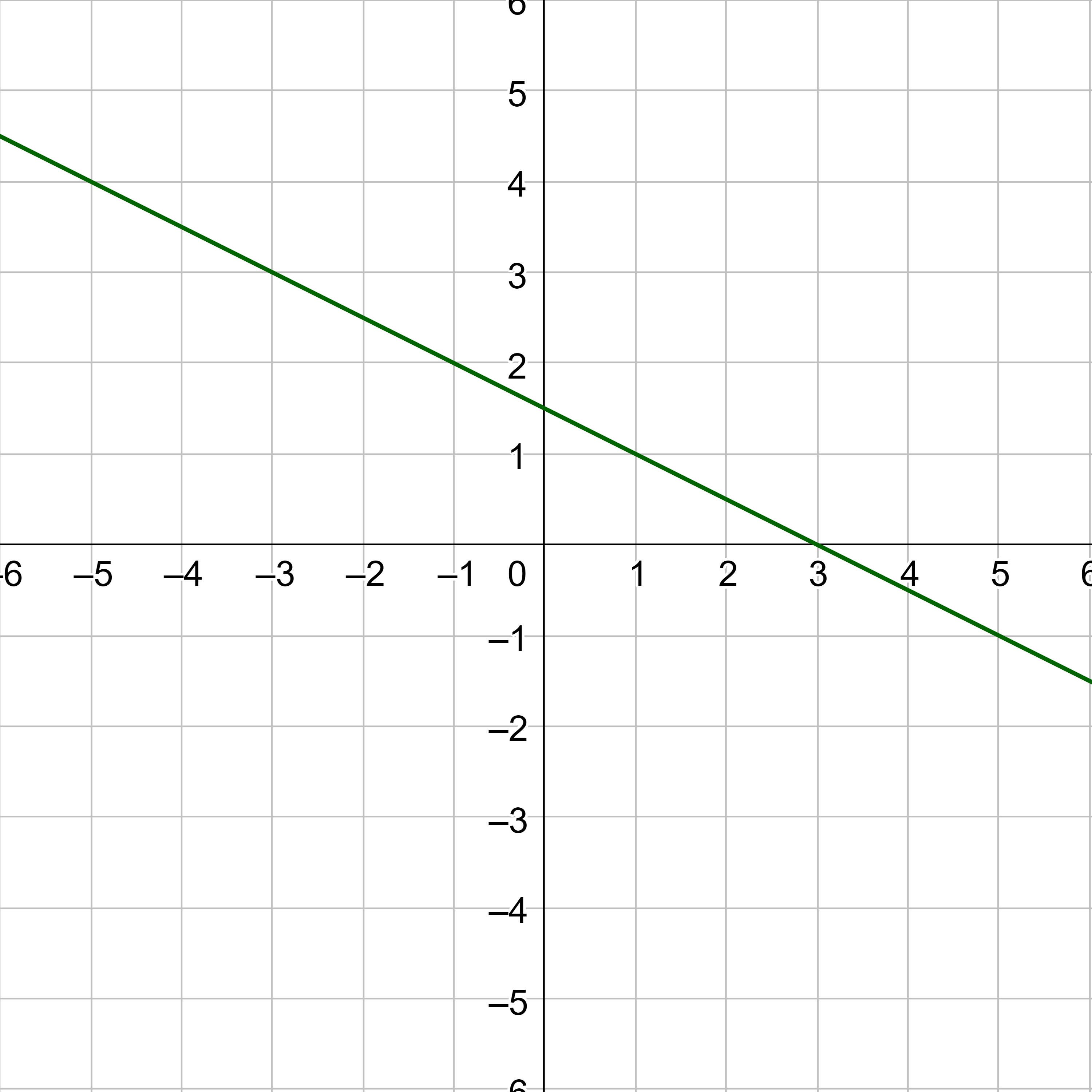
Find the equation of a line perpendicular to y = −2x + 1 that passes through the point (2, −1).

Solution

First find the slope. The question asks for a line perpendicular to the given line, and the slopes of perpendicular lines are the negative reciprocals. The slope of the given line is −2, so the slope of the desired line is \(m = \frac{1}{2}\).

The point (x₁, y₁) is (2, −1). Substitute those into the point-slope form of a line.

y − y₁ = m(x − x₁)

$$ y - (-1) = \frac{1}{2}(x - 2) $$

Distribute.

$$ y + 1 = \frac{1}{2}x - 1 $$

$$ y = \frac{1}{2}x - 2 $$

To illustrate that the lines are in fact perpendicular, figure 8 shows the graphs of both lines.

Graph Linear Functions

Does the equation of a line provide a quick way to graph lines other than making a table? Slope-intercept form is convenient because it contains a point, the y-intercept. To graph the line, start by plotting the y-intercept. Then the slope, rise/run, indicates the direction of the line, so move up the rise and over to the right the distance of the run and plot another point. Repeat for a few more points. If the slope is negative, the motion is down and the right. Finally, draw the line through the points.

Graph by Using the y-intercept and Slope

Graph y = −2x − 1 using the y-intercept and slope.

Solution

The equation is already solved for y and is in slope-intercept form. Compare it to y = mx + b. m = −2 and b = −1. Start by plotting the y-intercept, (0, b) = (0, −1).

Next follow the slope from that point to get a couple more points. The slope, m, is −2 or \(-\frac{2}{1}\). This is the rise/run, so the rise is −2 and the run is 1. From the y-intercept, move down 2 and right 1 to get a couple points. Or move the exact opposite, up 2 and left 1. Finally draw a line through the points.

Graph \(y = \frac{2}{3}x + 2\) using the y-intercept and slope.

Answer

Describe Horizontal and Vertical Lines

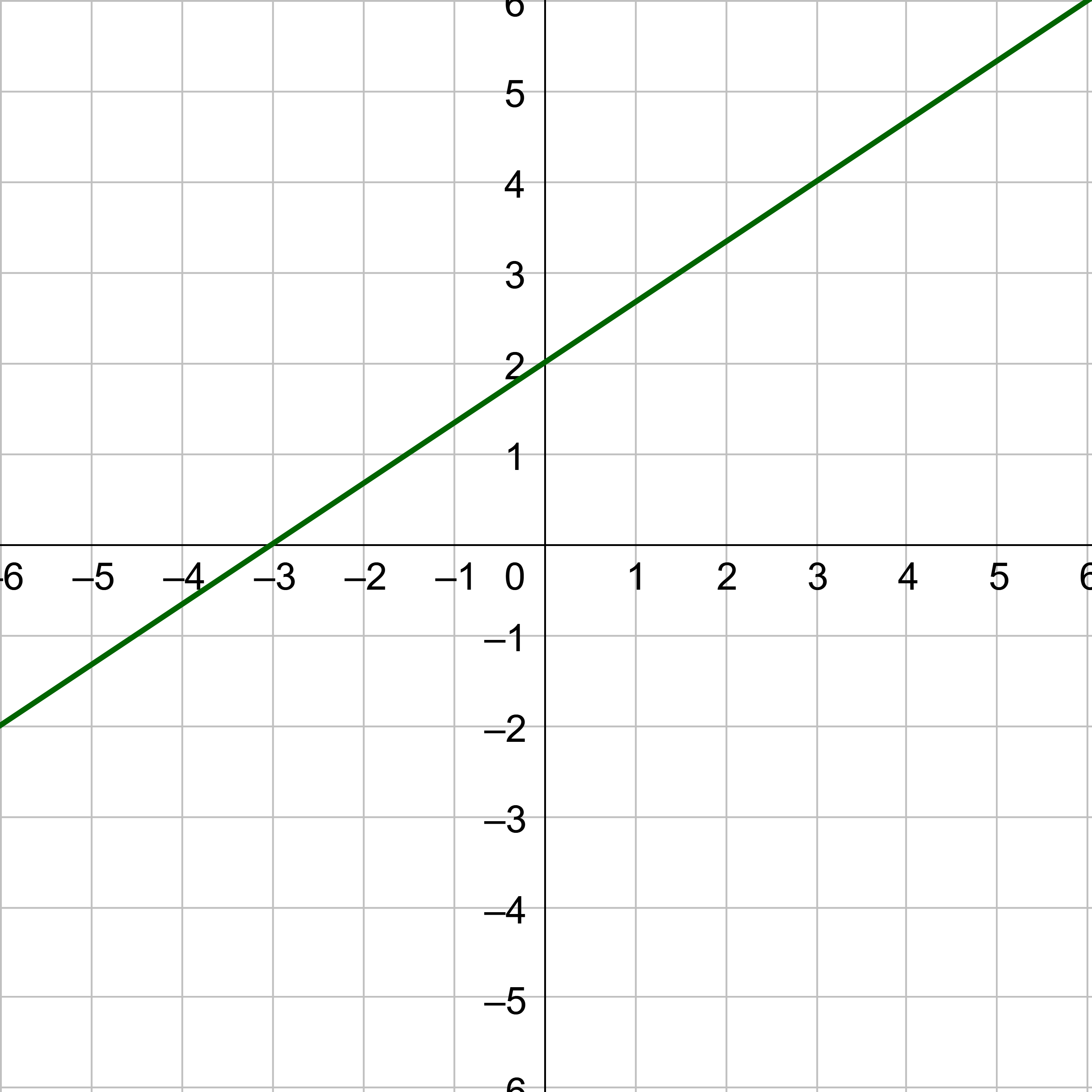
Two special lines have slightly different equations: horizontal and vertical lines. Horizontal lines have zero slope and a constant value. They have zero slope because there is no rise, so rise/run = 0/run = 0. The equation of a horizontal line is y = b where (0, b) is the y-intercept.

Vertical lines have no slope, sometimes called undefined slope, because they have zero run. The slope is rise/run = rise/0. Dividing by zero is undefined, so there is no slope. The x-value of the line is constant. The equation of a vertical line is x = a.

Write the Equation of a Vertical Line

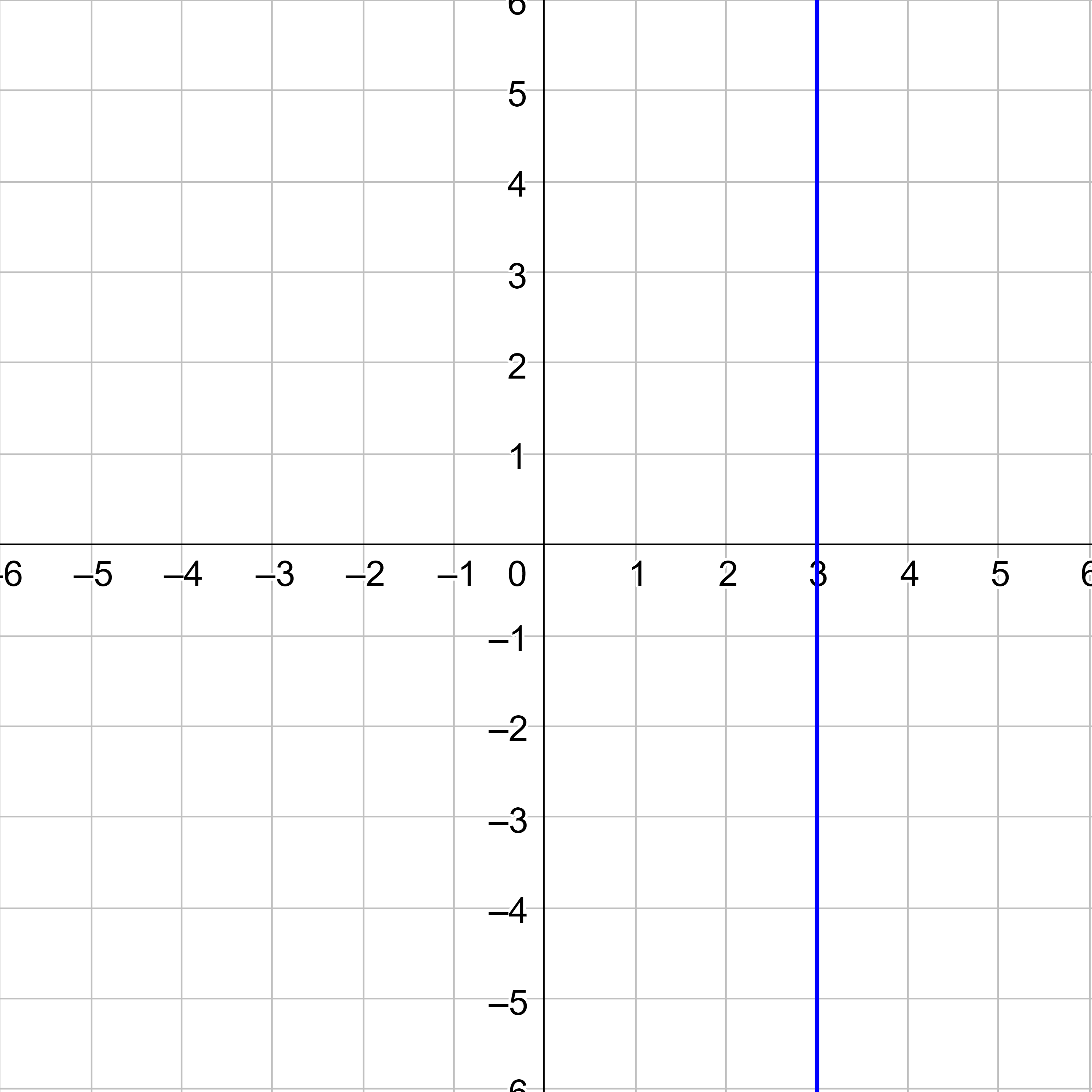
Write the equation of the line graphed in the figure.

Solution

It is a vertical line, so it is in the form x = a. The constant x-value is −2, so the equation is x = −2.

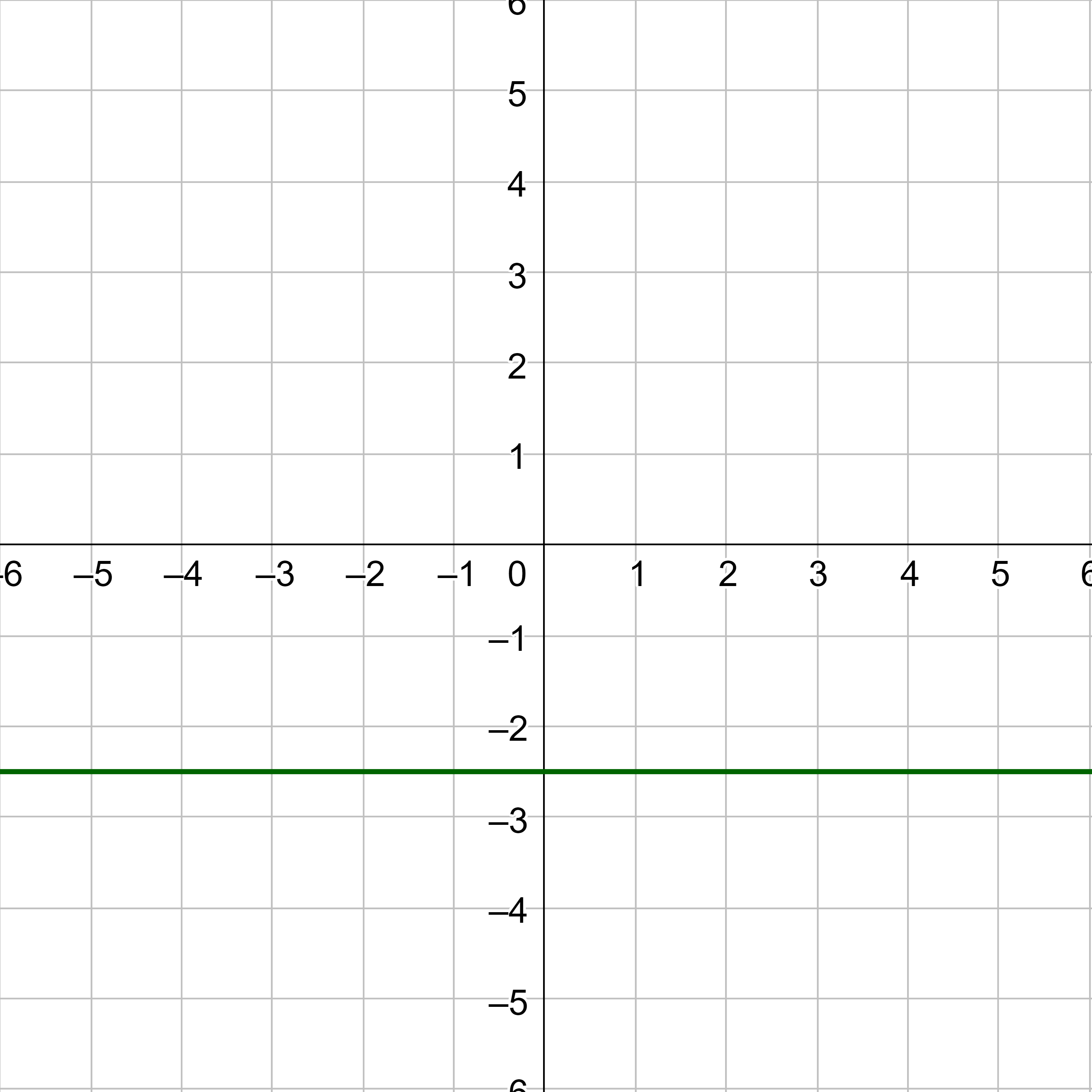
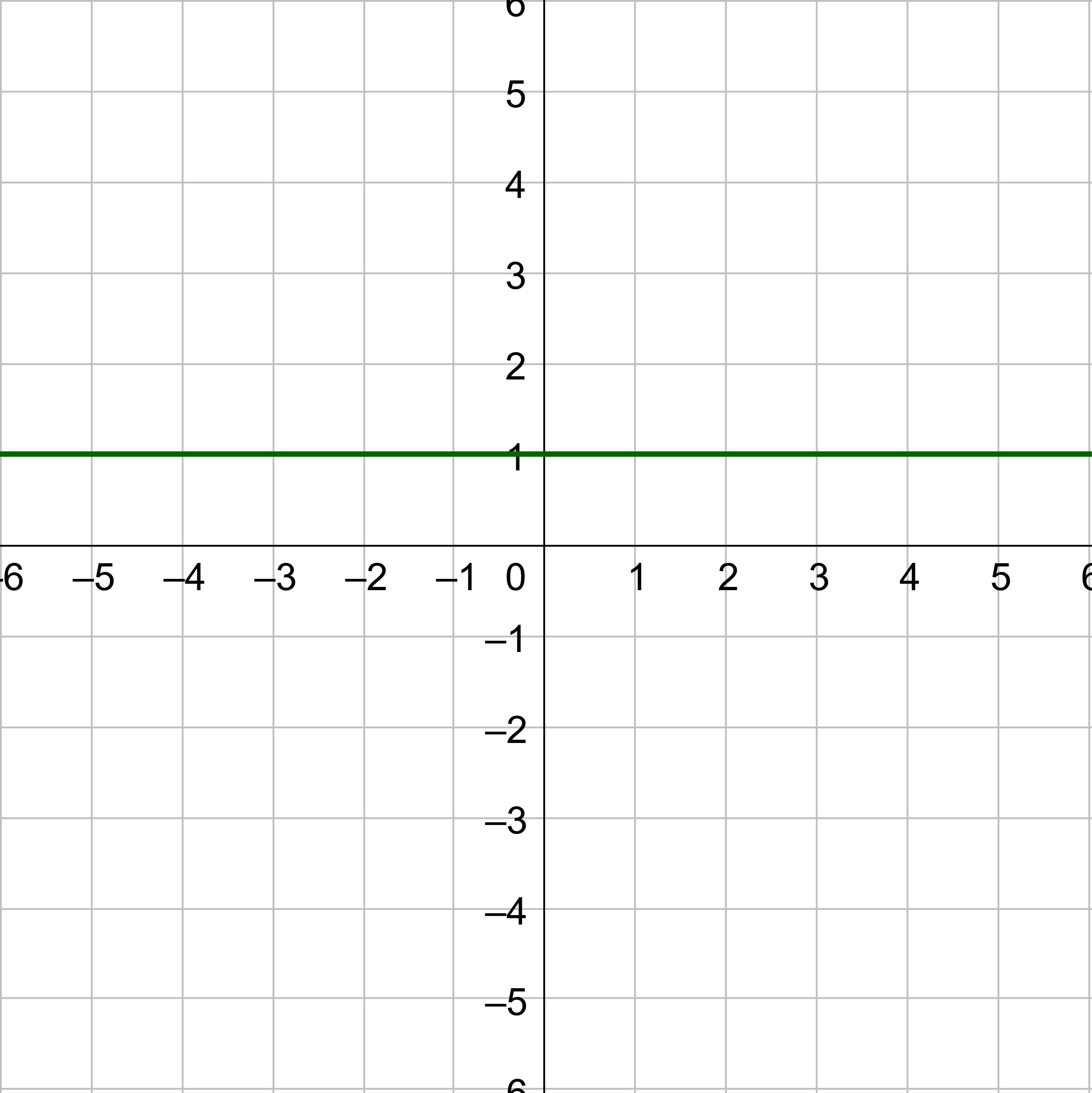
Graph y = 1

Answer

Applications

Practice Exercises (*Optional)

1. What is the relationship between the (a) slopes and (b) y-intercepts of two parallel lines?
2. If a vertical line has the equation x = 3 and a horizontal line has the equation y = 1, what is the point of intersection? Why?
3. Explain how to find a line perpendicular to a linear function that passes through a given point.
4. Find the slope from the graph.
   

   

5. Find the slope of the line passing through (2, −3) and (−1, 4).
6. Write the equation of the line with the following characteristics.
7. Slope of 2 and y-intercept of −14
8. Passing through (3, 8) and (−2, −4)
9. Passing through (−2, 1) and (1, −5)
10. Parallel to \(y = \frac{2}{3}x + 4\) and passing through (2, 1)
11. Perpendicular to \(y = -\frac{4}{3}x - \frac{1}{3}\) and passing through (4, −2)
12. Graph the equations.
13. x = 3
14. y = −2.5
15. y = −x + 1
16. \(y = \frac{1}{3}x - \frac{2}{3}\)
17. 2x + 4y = 6
18. Problem Solving
19. An airplane is coming in for a landing. Its altitude, A in feet, after t minutes can be modeled by A = 35,000 − 3,000t. Write a complete sentence describing the airplane's starting altitude and how it changes over time.
20. Francine is driving to her grandmother's house. After 10 minutes she is 70 miles away from grandmother's house. Later, 30 minutes after leaving, she is 50 miles away from grandmother's house. What is her rate in miles per hour?
21. Jamal wants to start a small business selling homemade jams. If the cost of the equipment is $250 and the cost of the ingredients and jar is $3.25 per jar, write an equation modeling Jamal's costs C as a function of jars of jam x.
22. Omar spent last summer selling cookbooks door to door. His costs of travel and lodging are $1500, but he makes a profit of $5 per book. Write an equation for Omar's profits.
23. *Sally has a rain gauge in her yard. It is now raining, and the gauge is filling up at 0.25 inches per hour. If there was 1 inch in the rain gauge before it started raining, write an equation for the level of water in Sally's rain gauge as a function of time.
24. *Todd is scuba diving in Mexico. He is a little low on air and needs to come back to the surface. He is 50 ft down and rises at about 0.5 ft/s. How long will it take Todd to get to the surface? (Alex A.)
25. The Canada Goose is a successful conservation story. After being hunted almost to extinction, the population is now very large. In 1970, about 9,000 Canada geese were counted in Michigan. In 2020, that number increased to over 300,000. What is the average rate of change of the goose population and what does it mean? (data: Michigan DNR)
26. Mixed Review
27. (1-02) Find the (a) center and (b) radius and (c) graph the circle (x + 2)² + (y − 1)² = 16
28. (1-02) Graph y = x² by first making a table.
29. (1-02) Find the x- and y-intercepts of 2x + 3y = 12
30. (1-01) Find the distance between (1, 2) and (−3, −1)
31. (1-01) Find the midpoint between (4, 9) and (0, 3)

Answers

1. The slopes are equal; y-intercepts are not equal.
2. The point of intersection is (3, 1). This is because for the horizontal line, all of the y coordinates are 1 and for the vertical line, all of the x coordinates are 3. The point of intersection will have these two characteristics.
3. First, find the slope of the given line. The slope of the perpendicular line is the negative reciprocal. Substitute the slope m of the perpendicular line and the coordinate of the given point into the equation y− y₁ = m(x − x₁) and solve for y.
4. \(-\frac{4}{3}\)
5. \(-\frac{7}{3}\)
6. y = 2x − 14
7. \(y = \frac{12}{5}x + \frac{4}{5}\)
8. y = −2x − 3
9. \(y = \frac{2}{3}x - \frac{1}{3}\)
10. \(y = \frac{3}{4}x − 5\)

11. 

12. 

13. 

14. 

15. 

16. The airplane's initial altitude is 35,000 feet and decreases by 3,000 feet per minute.
17. −60 miles per hour (She is getting closer to grandmother's house by 60 miles per hour.)
18. C = 3.25x + 250
19. P = 5x − 1500
20. d = 0.25t + 1
21. 100 seconds
22. 5820 geese per year. On average, the geese population increased by 5820 geese every year.
23. (−2, 1); 4;

    

24. 

25. (6, 0); (0, 4)
26. 5
27. (2, 6)