Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.

When the centurion and those with him who were guarding Jesus saw the earthquake and all that had happened, they were terrified, and exclaimed, “Surely he was the Son of God!” Matthew‬ ‭27‬:‭54‬ ‭NIV‬‬‬

4-06 Graphs of Sine and Cosine

The mass on the end of a Foucault pendulum moves as the earth moves. A graph of the displacement of the pendulum over time is in the shape of a wave and can be modeled with a sine or cosine function. This lesson is about graphing sine and cosine functions.

Graph of Sine and Cosine

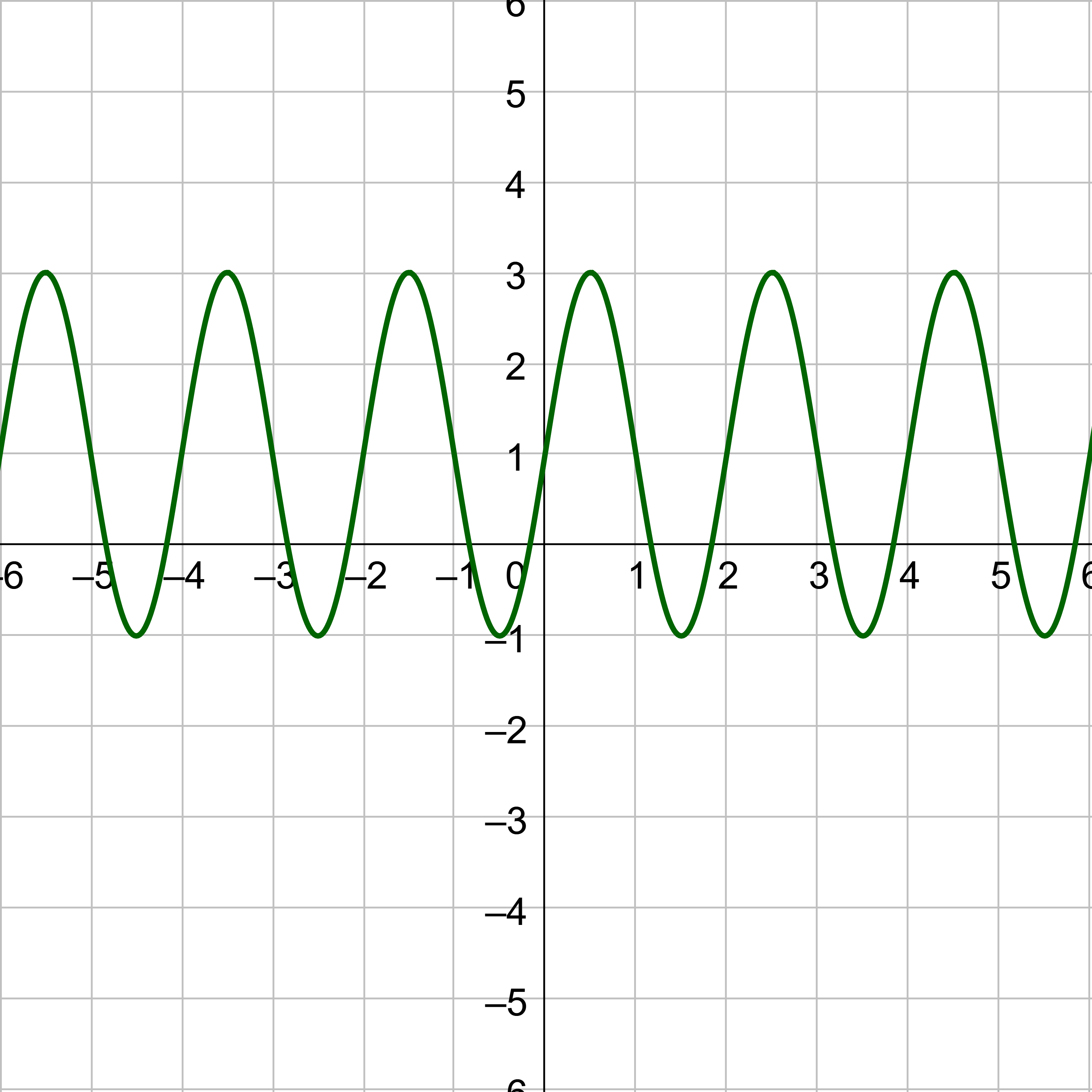
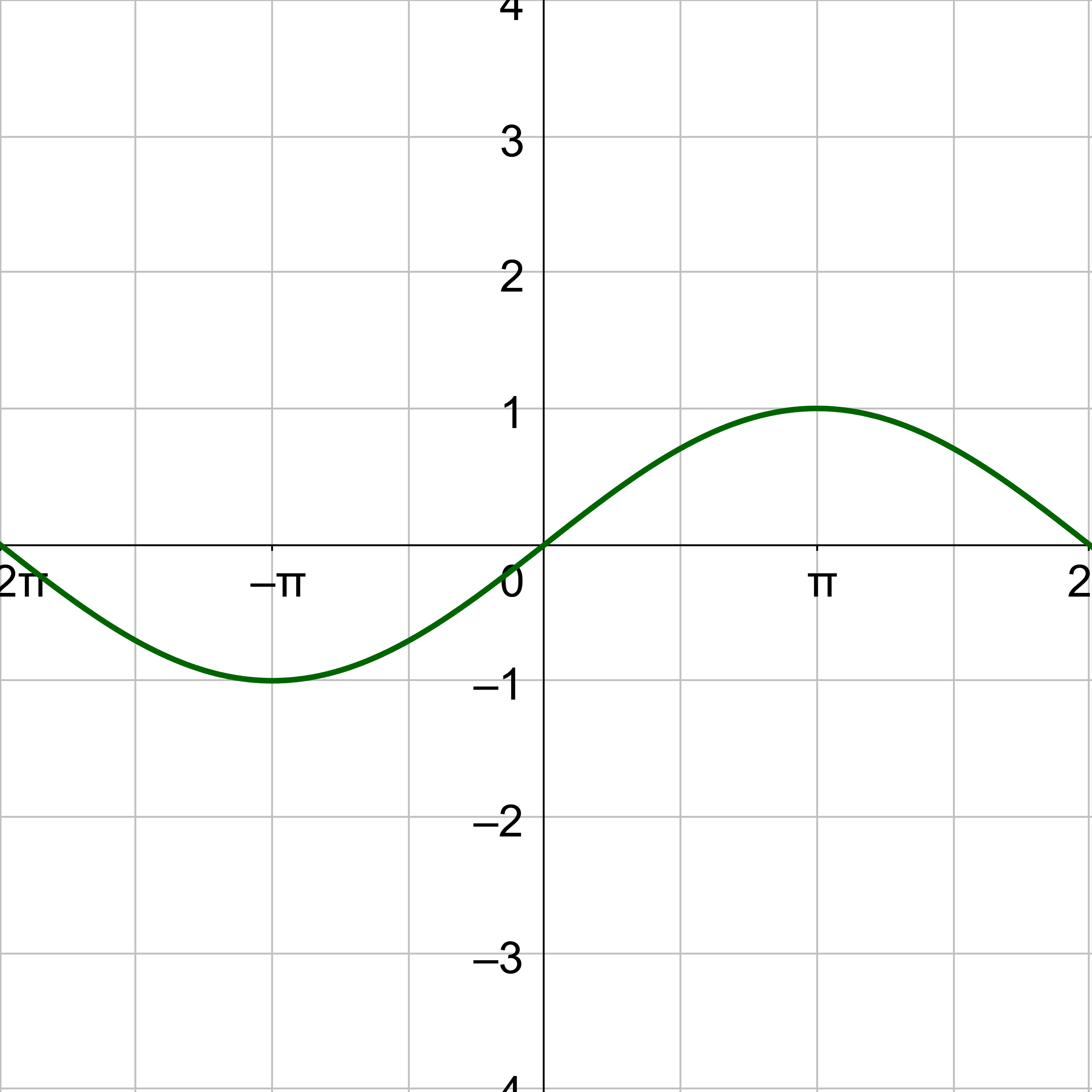
Consider the unit circle. Let x be the angle and y be the height above the x-axis on the unit circle. When y = sin x or y = cos x is graphed on the coordinate plane, this will produce a graph that looks like a wave as in figure 1. Notice the pattern repeats because the angle can move around the unit circle multiple times.

To graph a sine graph by hand, plot key points. The y-value of sine is zero at the angles of 0, π, and 2π. Sine equals 1 at π/2 and −1 at 3π/2. Plot those points on a coordinate plane and draw the wave. Repeat the wave pattern to complete the graph. Notice the maximum and minimum are halfway between zeros.

Cosine is the same shape as sine, only it starts at 1 instead of 0.

Transformations of Sine and Cosine Graphs

Amplitude

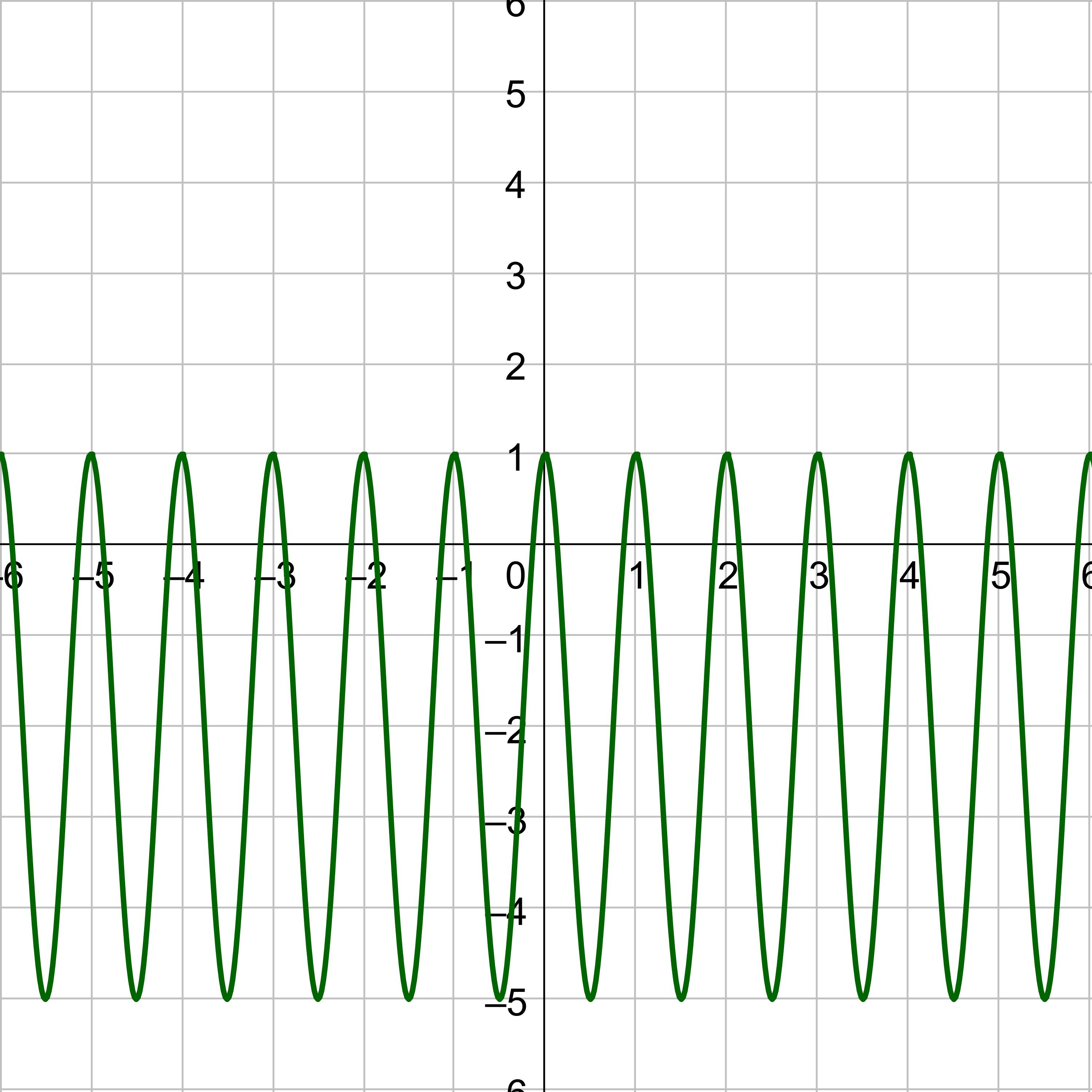
By multiplying a graph by a value, a, the graph is stretched vertically by a. This is because the function equals y, so if we multiply the function by a, then we multiply y by a. The original height of the sine or cosine graph is 1, the transformed height is a. This height is called the amplitude.

Example 2: Amplitude

Find the amplitude of y = 3 cos x.

Solution

Compare y = 3 cos x to y = a cos x. Notice that the a = 3, the amplitude is 3.

Period

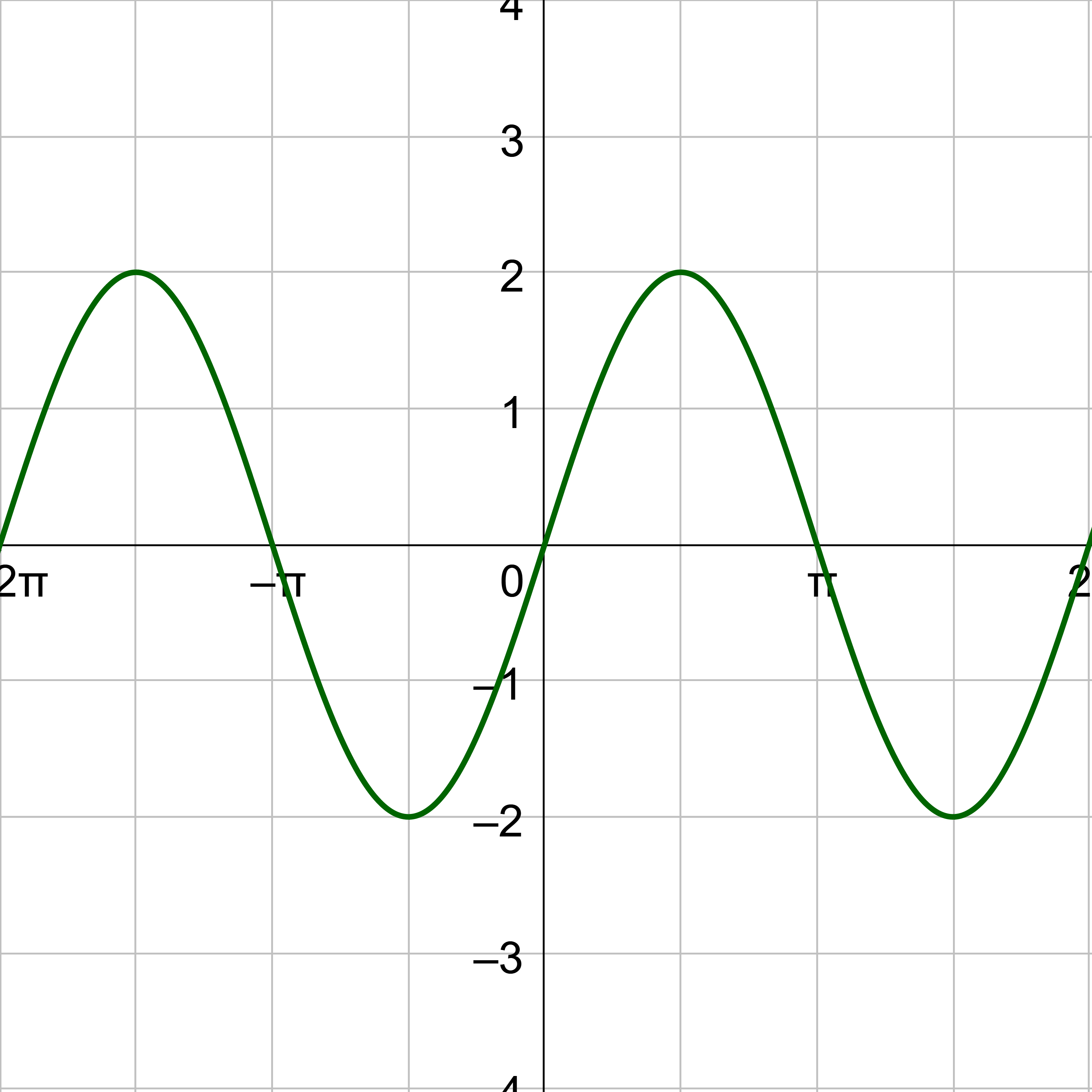
The distance on the x-axis of one full cycle of the graph is period. The period of the basic sine or cosine graph is 2π, but if the x is multiplied by a number, b, the graph is horizontally shrunk by the factor, b.

Example 3: Find the Period

Find the period of \(y = 2 \sin{\frac{1}{2}x}\).

Solution

By comparing \(y = 2 \sin{\frac{1}{2}x}\) to y = sin bx, b = \(\frac{1}{2}\). Calculate the period.

$\begin{array}{l}T=\frac{2\pi }{b}\\ T=\frac{2\pi }{\mathrm{½}}\\ T=4\pi \end{array}$

Phase Shift

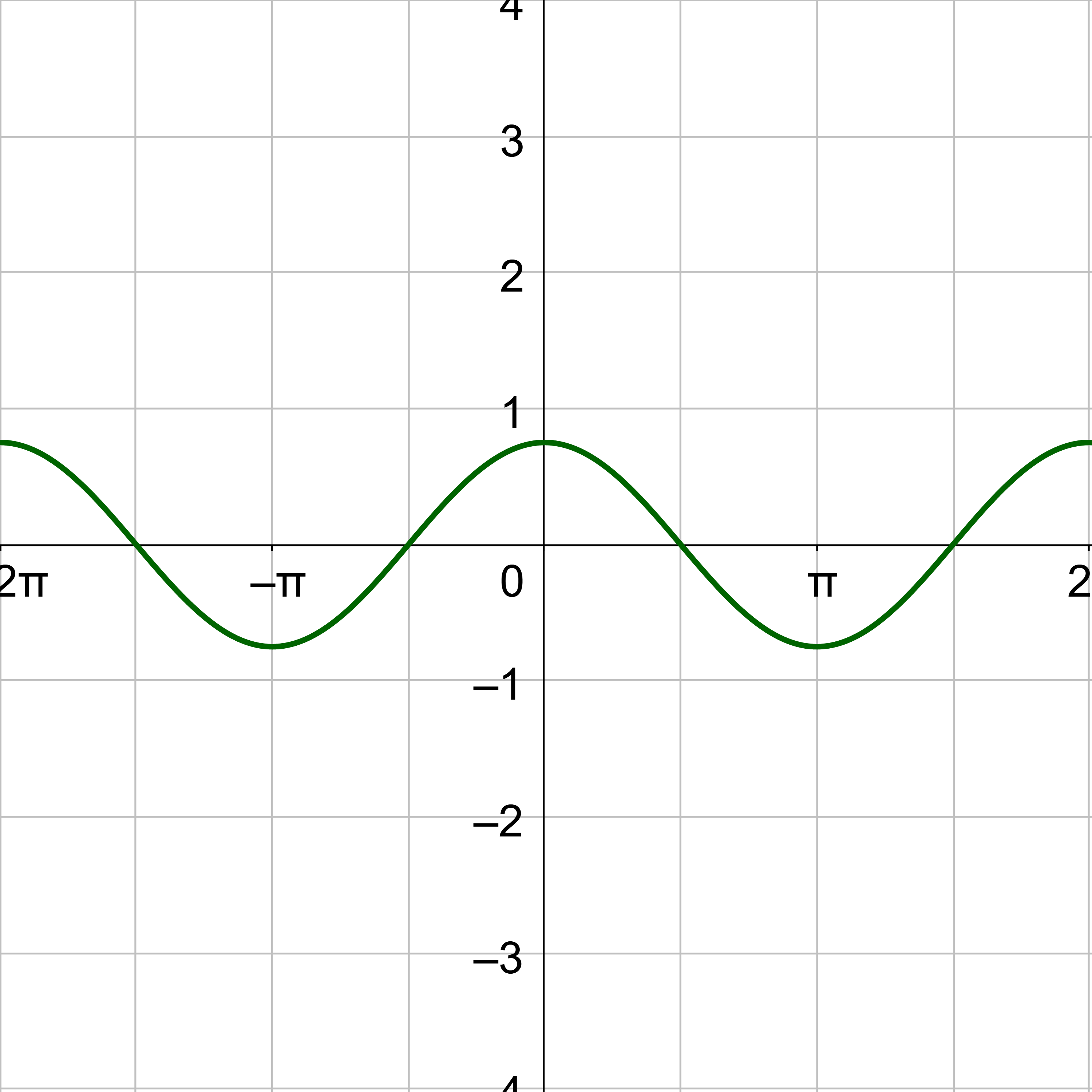
Graphs can be shifted horizontally. Since the horizontal is the x direction, to shift, or translate, the graph, add or subtract values to the x. This translation is called phase shift.

Example 4: Find Phase Shift

Find the phase shift of y = cos(2x + 6).

Solution

Compare y = cos(2x + 6) with y = cos(bx – c) to see b = 2 and c = −6. Calculate the phase shift.

$\begin{array}{l}\mathrm{PS}=\frac{c}{b}\\ \mathrm{PS}=\frac{-6}{2}\\ \mathrm{PS}=-3\end{array}$

Because the c is negative, the phase shift is 3 units to the left.

Midline

To shift a graph vertically, add a number to the entire function. Since the function equals y, adding a number to the function, adds the number to y. The middle of sine and cosine is usually at y = 0. Thus, the vertical translation is called the midline.

Transformations of Sine and Cosine

Put it all together.

Example 5: Sketch a Graph of Sine or Cosine

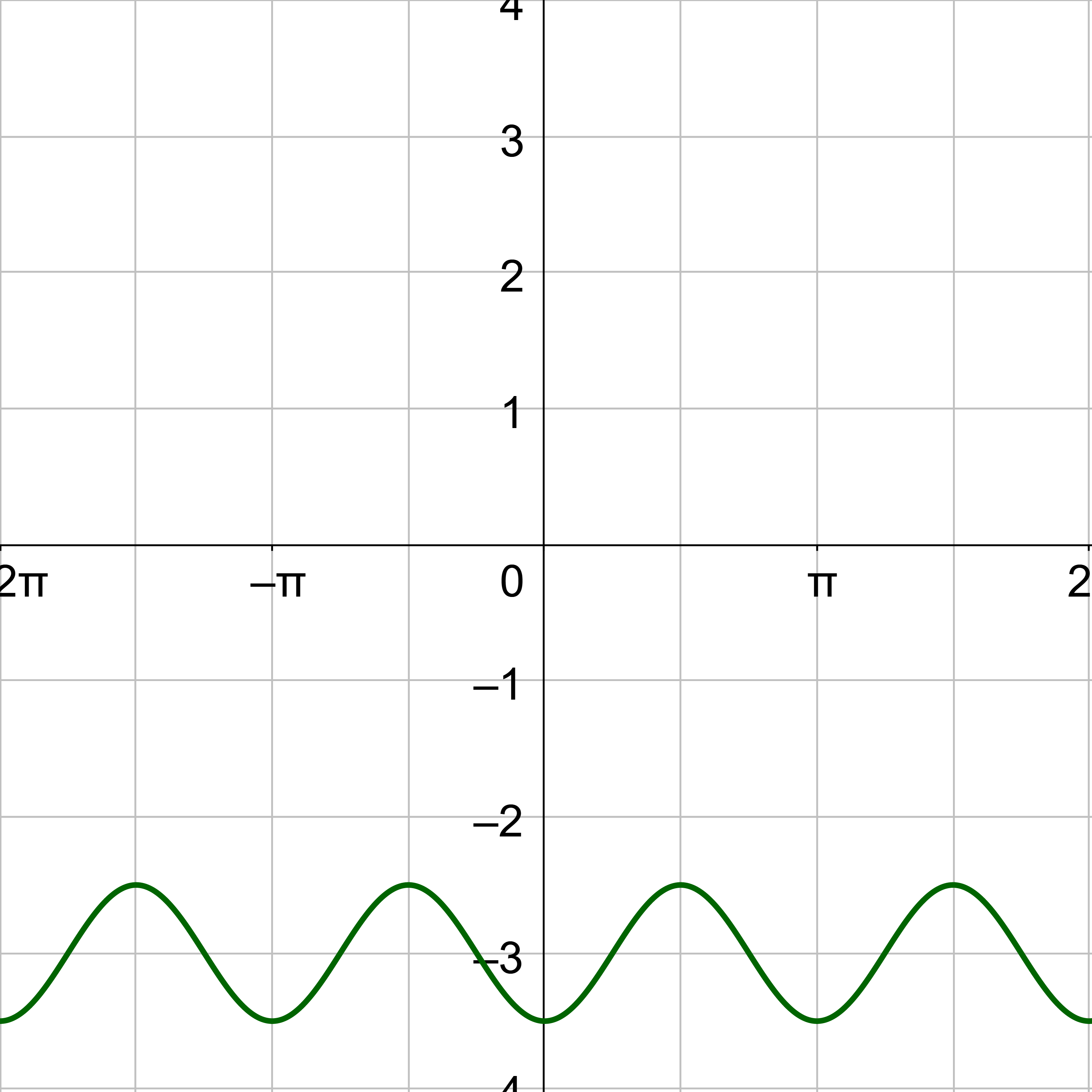
Graph y = sin (3x + π) + 1

Solution

Compare y = sin(3x + π) + 1 to y = a sin(bx − c) + d.

a = 1
b = 3
c = −π
d = 1

The midline is y = d, so y = 1. Draw this line on the graph as a light dotted line.

The amplitude is 1, so label the y-axis so the maximum of the curve is 1 above the midline, 2, and the minimum is 1 below the midline, 0.

The period is

$\begin{array}{l}T=\frac{2\pi }{b}\\ T=\frac{2\pi }{3}\end{array}$

The phase shift is

$\begin{array}{l}\mathrm{PS}=\frac{c}{b}\\ \mathrm{PS}=-\frac{\pi }{3}\\ \text{Or }\frac{\pi }{3}\text{ to the left}\end{array}$

The first key points for sine is at (0, 0), but it has shifted left \(\frac{π}{3}\) and up 1, so it is \(\left(-\frac{π}{3}, 1\right)\). The fifth key point is one period to the right or at \(\left(-\frac{π}{3} + \frac{2π}{3}, 1\right) = \left(\frac{π}{3}, 1\right)\). The middle key point is halfway between the 1^st and 5^th key points, (0, 1). The maximum is halfway between the 1^st and 3^rd key points and the amplitude higher, \(\left(-\frac{π}{6}, 2\right)\). The minimum is halfway between the 3^rd and 5^th key points and the amplitude lower, \(\left(\frac{π}{6}, 0\right)\).

Sketch the sine curve through the key points and continue the shape so it repeats at either end.

Example 6: Sketch a graph of Sine or Cosine

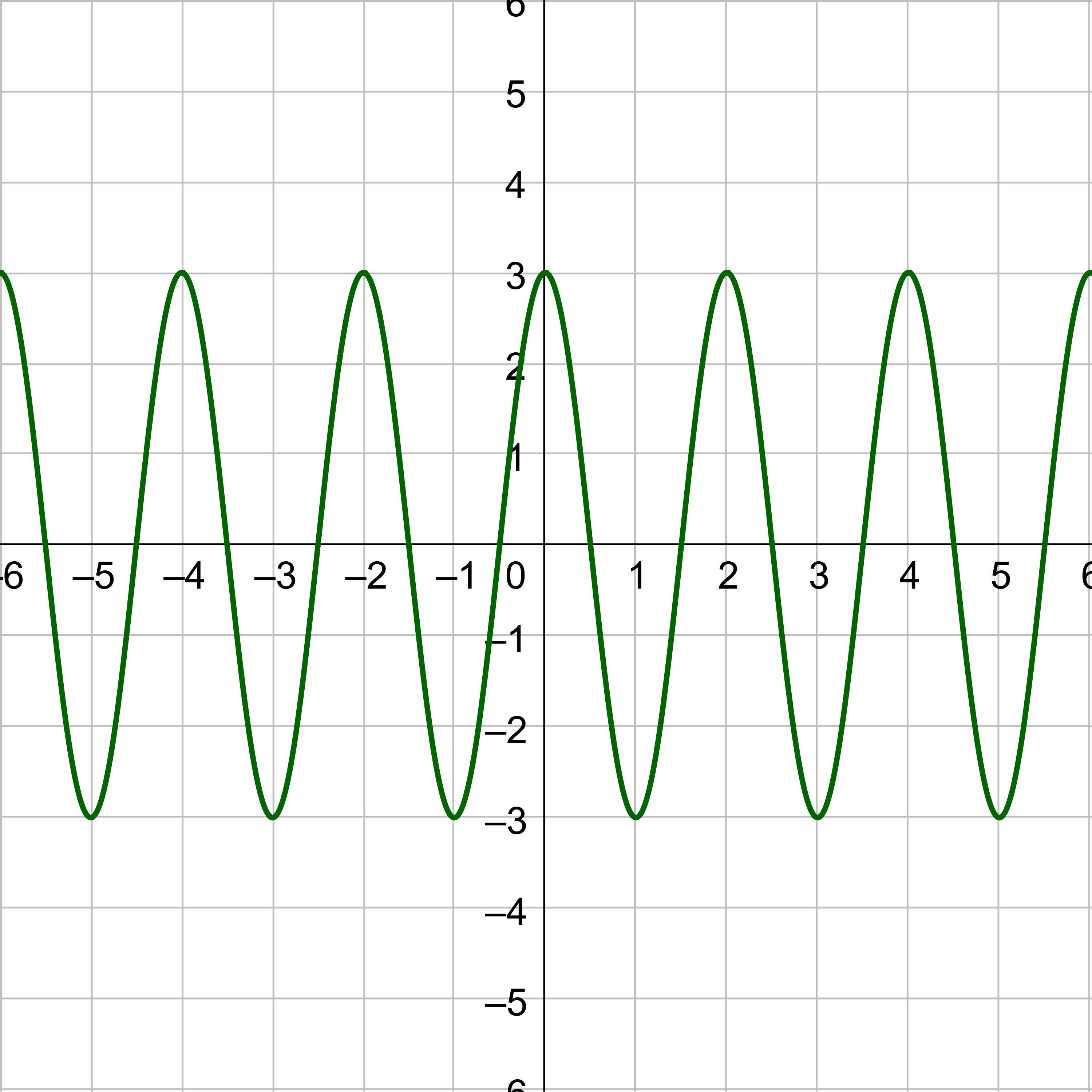
Sketch a graph of y = 4 cos(2x) – 3.

Solution

Compare y = 4 cos(2x) – 3 with y = a cos(bx − c) + d.

a = 4
b = 2
c = 0
d = −3

The midline is y = d, so y = −3. Draw this line on the graph as a light dotted line.

The amplitude is 4, so label the y-axis so the maximum of the curve is 4 above the midline, 1, and the minimum is 4 below the midline, −7.

The period is

$$ T = \frac{2π}{b} $$

$$ T = \frac{2π}{2} $$

$$ T = π $$

The phase shift is

$$ PS = \frac{c}{b} $$

$$ PS = \frac{0}{2} = 0 $$

The first key points for cosine is at (0, a), but it has shifted down 3, so it is (0, 4 − 1) = (0, 3). The fifth key point is one period to the right or at (0 + π, 3) = (π, 3). These are the maximums. The minimum is the middle key point and is halfway between the 1^st and 5^th key points but an amplitude below the midline, \(\left(\frac{π}{2}, -7\right)\). One zero is halfway between the 1^st and 3^rd key points on the midline, \(\left(\frac{π}{4}, -3\right)\). The other zero is halfway between the 3^rd and 5^th key points on the midline, \(\left(\frac{3π}{4}, -3\right)\).

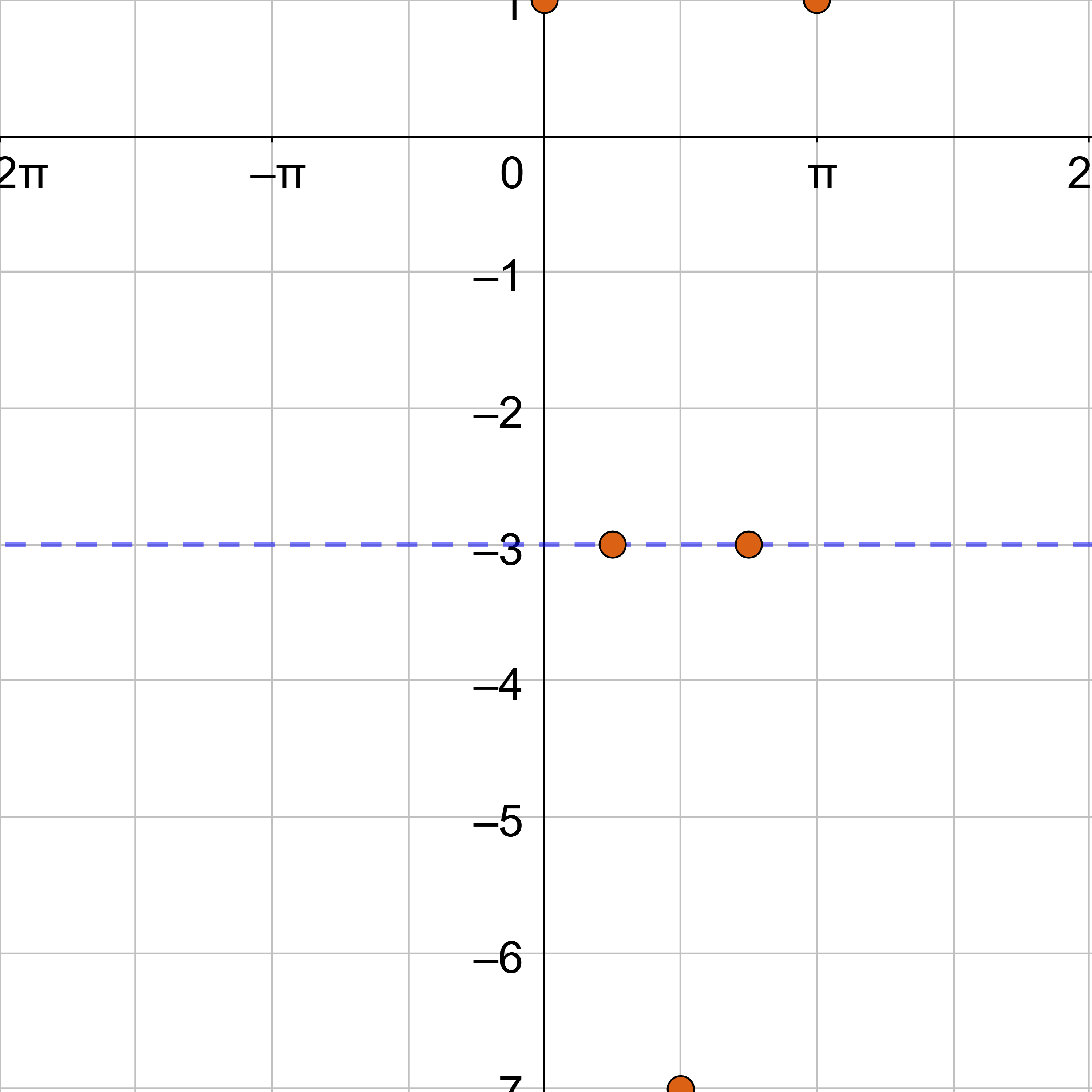
Sketch the sine curve through the key points and continue the shape so it repeats at either end.

Try It 4

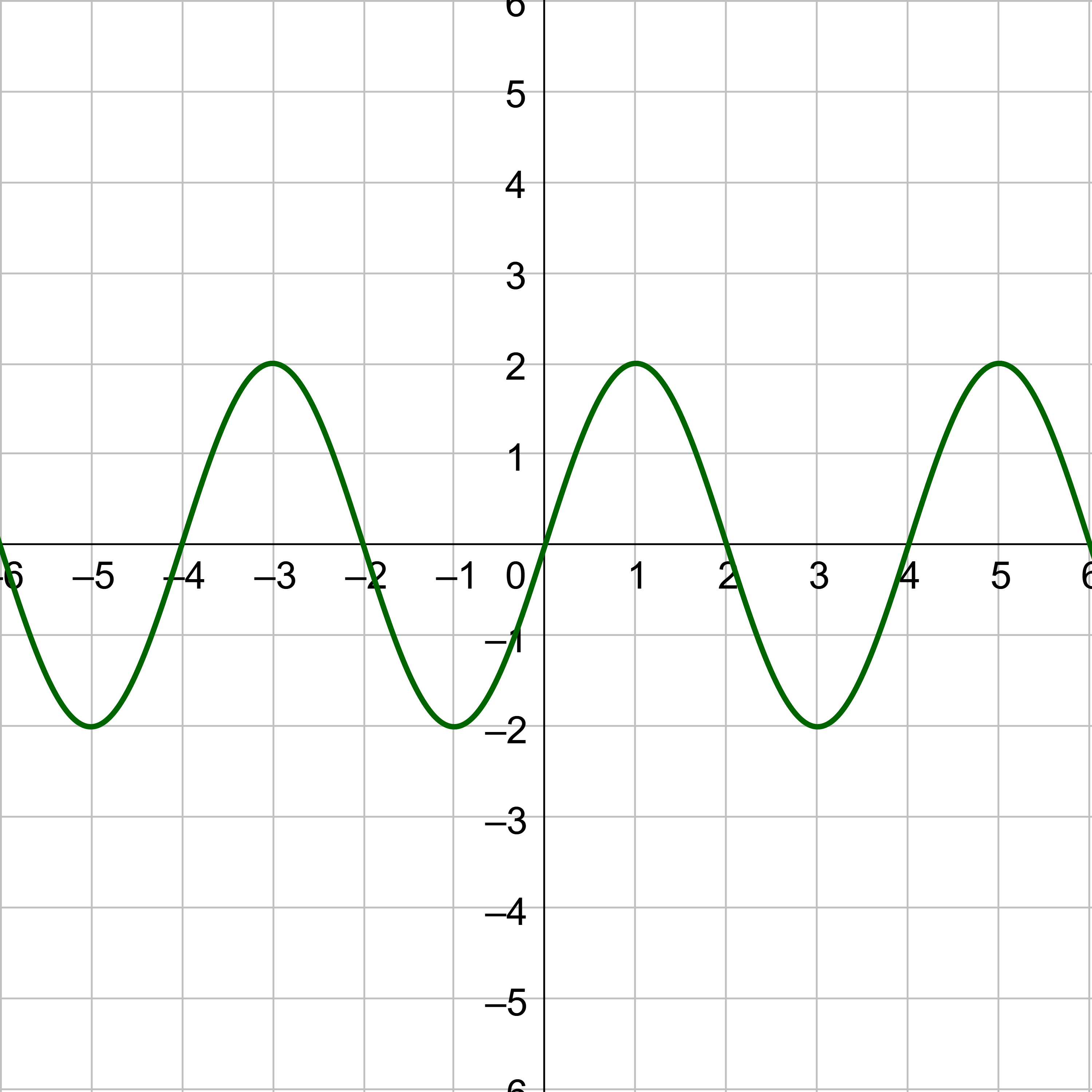
Sketch a graph of y = 2 sin(πx − π)

Answer

Modeling with Sine and Cosine

Periodic motion and other events that repeat can often be modeled with a sine or cosine function. To begin, decide if you want to use sine or cosine. If the data is zero at x = 0, use y = a sin(bx − c) + d. If the data is a maximum at x = 0, use y = a cos(bx − c) + d. Otherwise either sine or cosine will work. Second, determine the equilibrium, or middle, value by averaging the minimum and maximum values. This is the vertical translation, called the midline, y = d. Next determine the amplitude, a, by subtracting the maximum and the equilibrium values. Then determine the period by finding how long it takes to complete a full cycle. Calculate b using period = \(\frac{2π}{b}\). Finally find c by looking at the phase shift. If using sine, find when the first intercept occurs. If you are using cosine, find when the first maximum occurs. This is the phase shift, so use it to calculate c; \(PS = \frac{c}{b}\). Now fill in the formula to create the model.

Alternatively, to find c after you have found the a, b, and d, you could substitute a data point for x and y and solve for c.

Example 7: Write a Model

The London Eye is a huge Ferris wheel with a diameter of 120 meters (394 feet). It completes one rotation every 30 minutes. Riders board from a platform 15 meters above the ground. Express a rider's height above ground as a function of time in minutes.

Solution

Since passengers board at the lowest point, use cosine. Because the it starts at a minimum instead of a maximum make a negative.

With a diameter of 120 m, the wheel has a radius of 60 m. The height will oscillate with amplitude 60 m above and below the center.

Passengers board 15 m above ground level, so the center of the wheel must be located 60 + 15 = 75 m above ground level. The midline of the oscillation will be at 75 m.

The wheel takes 30 minutes to complete 1 revolution, so the height will oscillate with a period of 30 minutes.

Amplitude: 60, so a = −60
Midline: 75, so d = 75
Period: 30, so \(b = \frac{2π}{30} = \frac{π}{15}\)
Phase shift: 0

An equation for the rider’s height would be $y=-60cos\left(\frac{\pi }{15}t\right)+75$ where t is in minutes and y is measured in meters.

Try It 5

A weight is attached to a spring that is then hung from a board, as shown in figure 18. As the spring oscillates up and down, the position y of the weight relative to the board ranges from −1 in. (at time x = 0) to −7 in. (at time x = π) below the board. Assume the position of y is given as a sinusoidal function of x. Then find a cosine function that gives the position y in terms of x.

Answer

y = 3 cos(x) – 4

Practice Exercises

1. Why are sine and cosine called periodic functions?

Graph two full periods of each function and state the amplitude, period, and midline. State the maximum and minimum y-values and their corresponding x-values on one period for x > 0. State the phase shift and midline. Round answers to two decimal places if necessary.

2. y = 2 sin x
3. \(f(x) = \frac{3}{4} \cos x\)
4. \(g(x) = \sin \left(\frac{1}{2} x\right)\)
5. y = 3 cos(πx)
6. \(f(x) = -2 \sin\left(\frac{π}{2}x - π\right)\)
7. \(g(x) = -\frac{1}{2} \cos (2x) - 3\)
8. Determine the amplitude, midline, period, and an equation involving the sine function for the graph.
   
9. Determine the amplitude, period, midline, and an equation involving cosine for the graph.
   

10. 

    The Centennial Wheel is a large observational wheel in Chicago with a diameter of 196 ft. Passengers load at the bottom of the wheel from a platform that is 10 ft high. The wheel completes 3 revolutions in 15 minutes. Let h(t) be a function that gives the height of a passenger at time t.
    1. Find the amplitude, midline, and period of h(t).
    2. Find a formula for the height function h(t).
    3. How high off the ground is a person after 10 minutes?

Mixed Review

11. (4-05) Evaluate the function of θ. If $sin\theta =\frac{1}{3}$ and θ is in quadrant II, find a) cos θ and b) tan θ.
12. (4-05) Evaluate the six trigonometric function of θ = π.
13. (4-04) If cos θ = 0.8, find a) sin θ and b) cot θ using identities.
14. (4-03) Use special right triangles to evaluate the six trigonometric functions for $\frac{\pi }{3}$.
15. (4-02) Use the unit circle to evaluate the six trigonometric functions for $-\frac{\pi }{6}$.

Answers

1. The shape of the graph repeats regularly.
2. Amp = 2; T = 2π; y = 0; PS = 0; Max \(\left(\frac{π}{2}, 2\right)\); Min \(\left(\frac{3π}{2}, -2\right)\);
3. Amp = \(\frac{3}{4}\); T = 2π; y = 0; PS = 0; Max \(\left(2π, \frac{3}{4}\right)\); Min \(\left(π, -\frac{3}{4}\right)\);
4. Amp = 1; T = 4π; y = 0; PS = 0; Max (π, 1); Min (3π, −1);
5. Amp = 3; T = 2; y = 0; PS = 0; Max (2, 3); Min (1, −3);
6. Amp = 2; T = 4; y = 0; PS = 2 right; Max (1, 2); Min (3, −2);
7. Amp = \(\frac{1}{2}\); T = π; y = −3; PS = 0; Max \(\left(\frac{π}{2}, -\frac{5}{2}\right)\); Min \(\left(π, -\frac{7}{2}\right)\);
8. Amp = 2; T = 2; y = 1; PS = 0; y = 2 sin(πx) + 1
9. Amp = 3; T = 1; y = −2; PS = 0; y = 3 cos(2πx) − 2
10. (a) Amp = 98 ft; midline y = 108 ft; T = 5 min (b) \(h(t) = -98 \cos\left(\frac{2π}{5}t\right) + 108\) (c) 10 ft
11. $-\frac{2\sqrt{2}}{3}$; $-\frac{\sqrt{2}}{4}$
12. sin π = 0; cos π = −1; tan π = 0; csc π = und; sec π = −1; cot π = und
13. 0.6; 4/3
14. $\begin{array}{lll}sin\theta =\frac{\sqrt{3}}{2};& cos\theta =\frac{1}{2};& tan\theta =\sqrt{3};\\ csc\theta =\frac{2\sqrt{3}}{3};& sec\theta =2;& cot\theta =\frac{\sqrt{3}}{3}\end{array}$
15. $\begin{array}{lll}sin\theta =-\frac{1}{2};& cos\theta =\frac{\sqrt{3}}{2};& tan\theta =-\frac{\sqrt{3}}{3};\\ csc\theta =-2;& sec\theta =\frac{2\sqrt{3}}{3};& cot\theta =-\sqrt{3}\end{array}$