Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.


But I tell you, do not swear an oath at all: either by heaven, for it is God’s throne; or by the earth, for it is his footstool; or by Jerusalem, for it is the city of the Great King. And do not swear by your head, for you cannot make even one hair white or black. All you need to say is simply ‘Yes’ or ‘No’; anything beyond this comes from the evil one. Matthew 5:34-37 NIV

11-03 Cross Products

Mr. Wright teaches the lesson.

Summary: In this section, you will:

SDA NAD Content Standards (2018): PC.6.4

Dockland building
Dockland Building. (Wikicommons/NatiSythen)

The Dockland Building in Hamburg, Germany is shaped like a parallelogram. It is possible to use vectors representing two adjacent sides of the building to find the area of the sides of the building. This is done by finding the cross product of the vectors. There are two ways to multiply two vectors. The dot product gives a scalar answer, and the cross product gives a vector result.

Cross Products

The cross product gives a vector that is orthogonal to both the vectors that are multiplied together. It is found by using the determinant of a 3×3 matrix.

$$ \overset{\rightharpoonup}{u} × \overset{\rightharpoonup}{v} = \left| \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \end{matrix} \right| $$

Cross Product

If \(\overset{\rightharpoonup}{u} = \langle u_1, u_2, u_3 \rangle\) and \(\overset{\rightharpoonup}{v} = \langle v_1, v_2, v_3 \rangle\), then

$$ \overset{\rightharpoonup}{u} × \overset{\rightharpoonup}{v} = \left| \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \end{matrix} \right| $$

Find a Cross Product

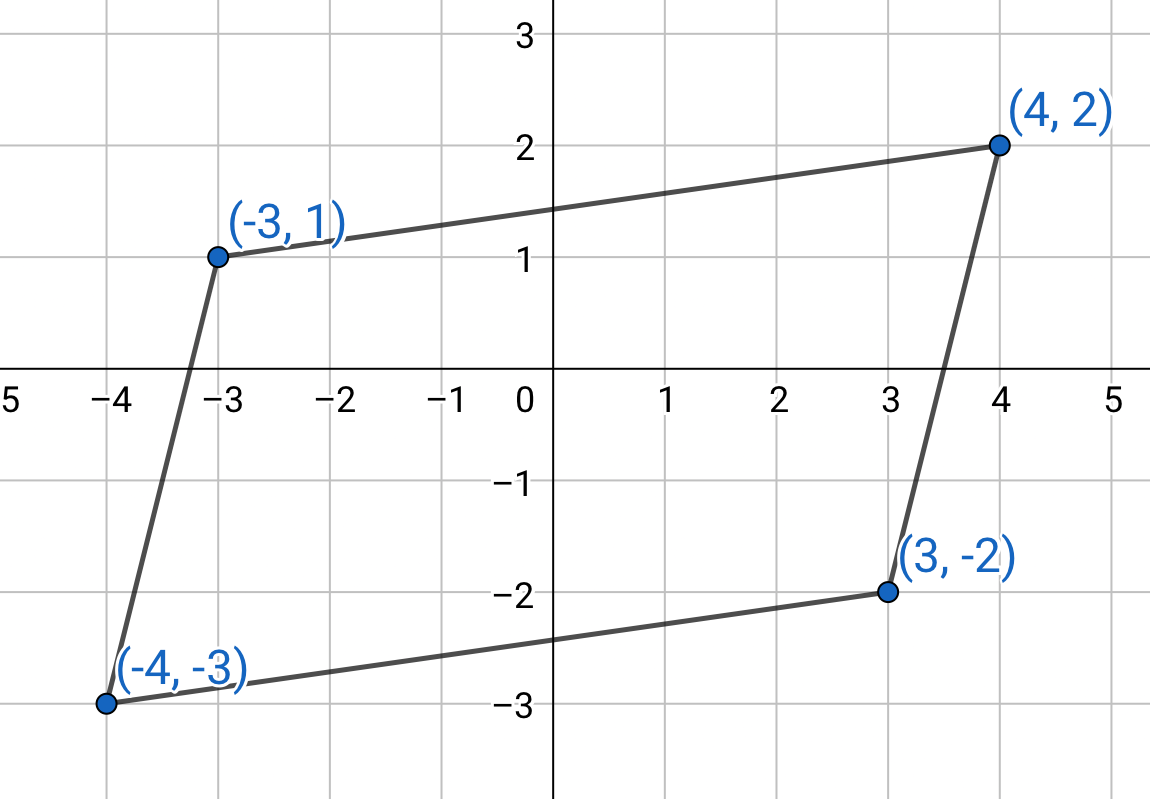
If \(\overset{\rightharpoonup}{u} = ⟨−2, 3, −3⟩\) and \(\overset{\rightharpoonup}{v} = ⟨1, −2, 1⟩\), find \(\overset{\rightharpoonup}{u} × \overset{\rightharpoonup}{v}\).

Solution

Set up the determinant.

$$ \overset{\rightharpoonup}{u} × \overset{\rightharpoonup}{v} = \left| \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \end{matrix} \right| $$

$$ \overset{\rightharpoonup}{u} × \overset{\rightharpoonup}{v} = \left|\begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ −2 & 3 & − 3 \\ 1 & −2 & 1 \end{matrix}\right| $$

Copy the first two columns to the end and find the determinant.

$$ \overset{\rightharpoonup}{u} × \overset{\rightharpoonup}{v} = \left|\begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ −2 & 3 & − 3 \\ 1 & −2 & 1 \end{matrix}\right| \begin{matrix} \hat{i} & \hat{j} \\ -2 & 3 \\ 1 & -2 \end{matrix} $$

$$ = 3\hat{i} + (−3)\hat{j} + 4\hat{k} − 3\hat{k} − 6\hat{i} − (−2)\hat{j} $$

$$ = −3\hat{i} − \hat{j} + \hat{k} $$

= ⟨−3, −1, 1⟩

Evaluate ⟨1, 4, −1⟩ × ⟨0, 3, −2⟩.

Answer

⟨−5, 2, 3⟩

Properties of Cross Products

Applications of Cross Products

Cross products can be used to find the area of a parallelogram.

parallelogram
Parallelogram

The area of a parallelogram is found by A = bh. The height can be found using trigonometry with the right triangle shown in the picture. The hypotenuse of the triangle is the magnitude of the vector representing the side of the parallelogram.

$$ h = \| \overset{\rightharpoonup}{u} \| \sin θ $$

The base of the parallelogram is the magnitude of the vector representing that side of the parallelogram. So the area formula becomes

$$ A = \| \overset{\rightharpoonup}{v} \| \| \overset{\rightharpoonup}{u} \| \sin θ $$

This the same as the magnitude of the cross product of the two vectors. Thus, the area of a parallelogram is the magnitude of the cross product of the vectors representing two adjacent sides of the parallelogram.

Area of a Parallelogram

$$ A = \| \overset{\rightharpoonup}{u} × \overset{\rightharpoonup}{v} \| $$

where \(\overset{\rightharpoonup}{u}\) and \(\overset{\rightharpoonup}{v}\) represent adjacent sides.

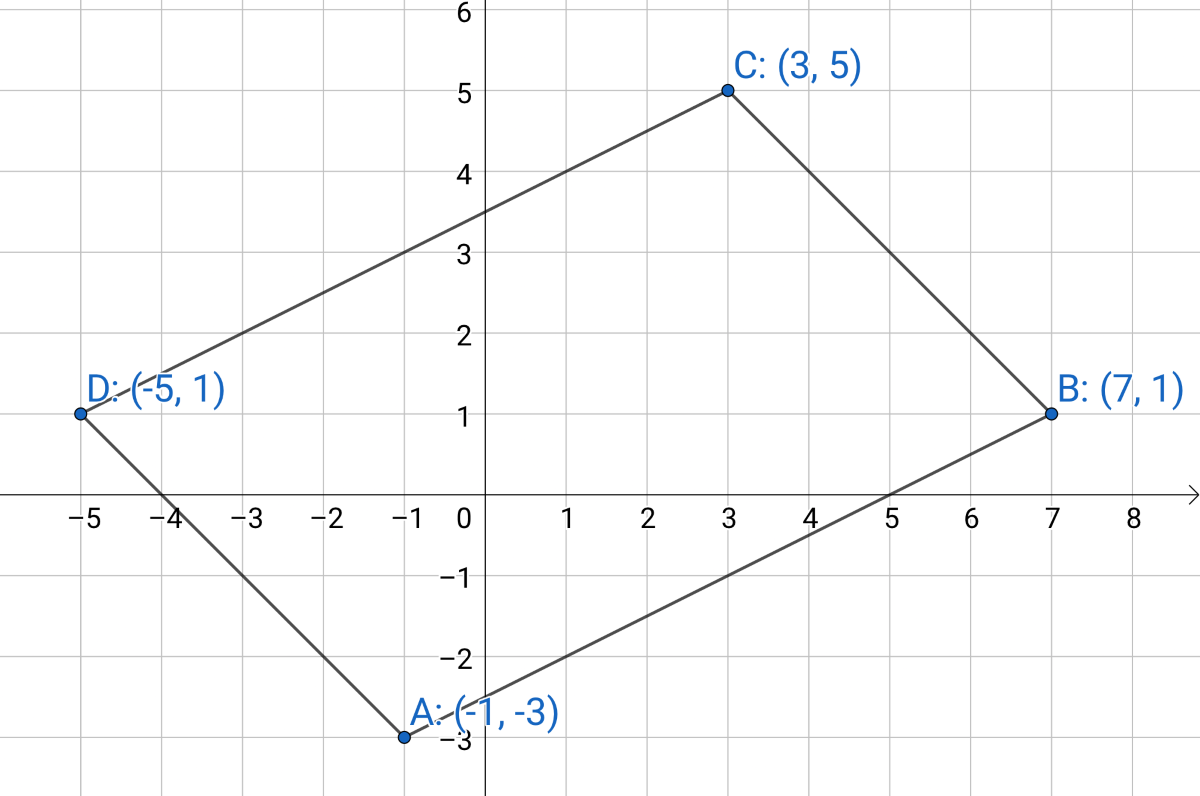
Area of a Parallelogram

Use a cross product to find the area of a parallelogram with vertices A(0, 0), B(4, 1), C(6, 3), D(2, 2).

Solution

Find vectors to represent adjacent edges, perhaps AB and AD.

$$ \overset{\rightharpoonup}{AB} = \langle 4-0, 1-0 \rangle \text{ and } \overset{\rightharpoonup}{AD} = \langle 2-0, 2-0 \rangle $$

$$ \overset{\rightharpoonup}{AB} = \langle 4, 1 \rangle \text{ and } \overset{\rightharpoonup}{AD} = \langle 2, 2 \rangle $$

The area of the parallelogram is the magnitude of the cross product of the vectors representing adjacent sides.

$$ A = \| \overset{\rightharpoonup}{u} × \overset{\rightharpoonup}{v} \| $$

Find the cross product of the sides.

$$ \overset{\rightharpoonup}{u} × \overset{\rightharpoonup}{v} = \left| \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ 4 & 1 & 0 \\ 2 & 2 & 0 \end{matrix} \right| $$

$$ \overset{\rightharpoonup}{u} × \overset{\rightharpoonup}{v} = \left| \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ 4 & 1 & 0 \\ 2 & 2 & 0 \end{matrix} \right| \begin{matrix} \hat{i} & \hat{j} \\ 4 & 1 \\ 2 & 2 \end{matrix} $$

$$ \overset{\rightharpoonup}{u} × \overset{\rightharpoonup}{v} = 0\hat{i} + 0\hat{j} + 8\hat{k} - 2\hat{k} - 0\hat{i} - 0\hat{j} $$

$$ \overset{\rightharpoonup}{u} × \overset{\rightharpoonup}{v} = 6\hat{k} = \left\langle 0, 0, 6 \right\rangle $$

Now find the magnitude of the cross product. Since the cross product only has one component, its magnitude is the size of that component. The area of the parallelogram is 6.

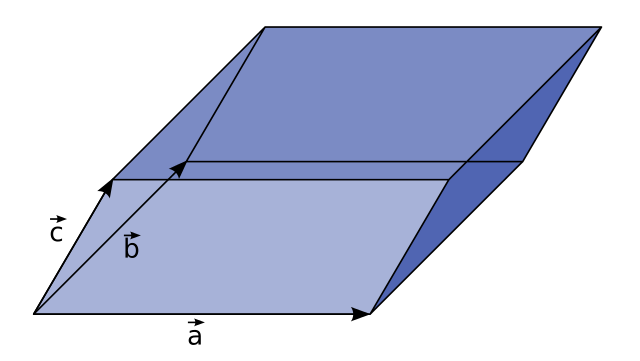
There are two different ways to multiply two vectors: the dot product and the cross product. Three vectors can be multiplied using both operations. The cross product would have to be done first so that the result is still a vector. Then the dot product could be calculated. This is called a triple scalar product and the shortcut for calculating it is

$$ \overset{\rightharpoonup}{u} \cdot (\overset{\rightharpoonup}{v} \times \overset{\rightharpoonup}{w}) = \left|\begin{matrix} u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \\w_1 & w_2 & w_3 \end{matrix} \right| $$

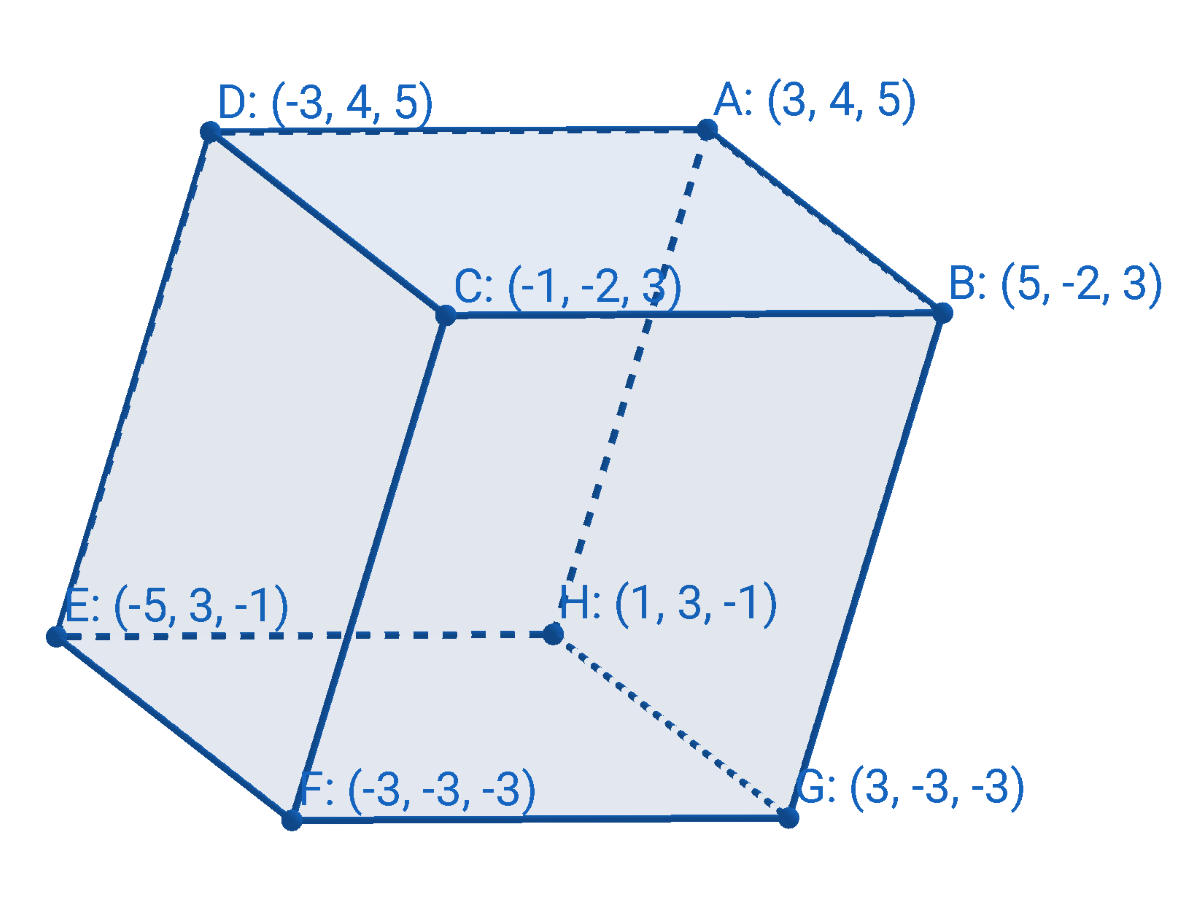
If the vectors represent adjacent edges of a parallelepiped, then the volume of it is the absolute value of the triple scalar product. A parallelepiped is like a three-dimensional parallelogram. Each of the faces are parallelograms, and opposite faces are congruent and parallel.

Triple Scalar Product

$$ \overset{\rightharpoonup}{u} \cdot (\overset{\rightharpoonup}{v} \times \overset{\rightharpoonup}{w}) = \left|\begin{matrix} u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \\w_1 & w_2 & w_3 \end{matrix} \right| $$

Volume of a Parallelepiped

$$ V = \left|\overset{\rightharpoonup}{a} \cdot (\overset{\rightharpoonup}{b} \times \overset{\rightharpoonup}{c}) \right| $$

where the vectors represent adjacent edges

Parallelepiped
Vectors representing edges of a parallelepiped (wikimedia\Niabot)

Triple Scalar Product

Evaluate \(\overset{\rightharpoonup}{a} \cdot (\overset{\rightharpoonup}{b} \times \overset{\rightharpoonup}{c})\) if \(\overset{\rightharpoonup}{a} = \langle 2, -3, 1 \rangle\), \(\overset{\rightharpoonup}{b} = \langle 3, -1, 0 \rangle\), and \(\overset{\rightharpoonup}{c} = \langle 0, -2, 4 \rangle\).

Solution

Let's use the shortcut method. Fill the components of the vectors into a determinant.

$$ \overset{\rightharpoonup}{a} \cdot (\overset{\rightharpoonup}{b} \times \overset{\rightharpoonup}{c}) = \left|\begin{matrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\c_1 & c_2 & c_3 \end{matrix} \right| $$

$$ = \left|\begin{matrix} 2 & -3 & 1 \\ 3 & -1 & 0 \\ 0 & -2 & 4 \end{matrix} \right| $$

Evaluate the determinant as learned in lesson 9-05. Start by copying the first two columns.

$$ = \left|\begin{matrix} 2 & -3 & 1 \\ 3 & -1 & 0 \\ 0 & -2 & 4 \end{matrix} \right| \begin{matrix} 2 & -3 \\ 3 & -1 \\ 0 & -2 \end{matrix} $$

Add the products of the downward diagonals with the products of the upward diagonals.

= (−8) + 0 + (−6) − 0 − 0 − (−36)

= 22

Evaluate \(\overset{\rightharpoonup}{p} \cdot (\overset{\rightharpoonup}{q} \times \overset{\rightharpoonup}{r})\) if \(\overset{\rightharpoonup}{p} = -2\hat{i} - \hat{j}\), \(\overset{\rightharpoonup}{q} = \hat{i} - 2\hat{j} + 2\hat{k}\), and \(\overset{\rightharpoonup}{r} = \hat{i} - 2\hat{j} + 3\hat{k}\).

Answer

5

Lesson Summary
Cross Product

If \(\overset{\rightharpoonup}{u} = \langle u_1, u_2, u_3 \rangle\) and \(\overset{\rightharpoonup}{v} = \langle v_1, v_2, v_3 \rangle\), then

$$ \overset{\rightharpoonup}{u} × \overset{\rightharpoonup}{v} = \left| \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \end{matrix} \right| $$

Properties of Cross Products
Area of a Parallelogram

$$ A = \| \overset{\rightharpoonup}{u} × \overset{\rightharpoonup}{v} \| $$

where \(\overset{\rightharpoonup}{u}\) and \(\overset{\rightharpoonup}{v}\) represent adjacent sides.

Triple Scalar Product

$$ \overset{\rightharpoonup}{u} \cdot (\overset{\rightharpoonup}{v} \times \overset{\rightharpoonup}{w}) = \left|\begin{matrix} u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \\w_1 & w_2 & w_3 \end{matrix} \right| $$

Volume of a Parallelepiped

$$ V = \left|\overset{\rightharpoonup}{a} \cdot (\overset{\rightharpoonup}{b} \times \overset{\rightharpoonup}{c}) \right| $$

where the vectors represent adjacent edges

Parallelepiped
Vectors representing edges of a parallelepiped (wikimedia\Niabot)

Helpful videos about this lesson.

Practice Exercises

  1. Given that \(\overset{\rightharpoonup}{m} = 2\hat{i} + \hat{j} - 2\hat{k}\) and \(\overset{\rightharpoonup}{n} = \hat{i} - 3\hat{k}\), evaluate the following.
  2. \(\overset{\rightharpoonup}{m} \times \overset{\rightharpoonup}{n}\)
  3. \(2(\overset{\rightharpoonup}{n}) \times \overset{\rightharpoonup}{m}\)
  4. \(\overset{\rightharpoonup}{n} \times \overset{\rightharpoonup}{n}\)
  5. \((\overset{\rightharpoonup}{n} \times \overset{\rightharpoonup}{m}) \times \overset{\rightharpoonup}{m}\)
  6. \(\overset{\rightharpoonup}{m} \cdot (\overset{\rightharpoonup}{m} \times \overset{\rightharpoonup}{n})\)
  7. Find the cross product of the vectors.
  8. ⟨3, 2, −4⟩ and ⟨0, −1, 2⟩
  9. ⟨−1, 4, 10⟩ and ⟨2, 1, 3⟩
  10. Find a unit vector that orthogonal to \(\overset{\rightharpoonup}{u}\) and \(\overset{\rightharpoonup}{v}\).
  11. \(\overset{\rightharpoonup}{u} = \langle 3, -1, 1 \rangle\) and \(\overset{\rightharpoonup}{v} = \langle -2, 0, 1 \rangle\)
  12. \(\overset{\rightharpoonup}{u} = \langle 0, 2, 0 \rangle\) and \(\overset{\rightharpoonup}{v} = \langle -1, 1, 1 \rangle\)
  13. \(\overset{\rightharpoonup}{u} = \langle 10, 15, -5 \rangle\) and \(\overset{\rightharpoonup}{v} = \langle -1, 3, -2 \rangle\)
  14. Use cross products to find the area of the parallelogram.
  15. parallelogram
  16. parallelogram
  17. Evaluate the triple scalar product of the three vectors.
  18. \(\begin{align} \overset{\rightharpoonup}{u} &= 2\hat{i} + 5\hat{j} - \hat{k} \\ \overset{\rightharpoonup}{v} &= \hat{i} + \hat{k} \\ \overset{\rightharpoonup}{w} &= -3\hat{i} -2\hat{j} + 2\hat{k} \end{align}\)
  19. \(\begin{align} \overset{\rightharpoonup}{a} &= \langle 2, 5, 1 \rangle \\ \overset{\rightharpoonup}{b} &= \langle 0, -2, 4 \rangle \\ \overset{\rightharpoonup}{c} &= \langle 0, 2, 0 \rangle \end{align}\)
  20. Find the volume of the parallelepiped.
  21. parallelogram
  22. Problem Solving
  23. Dockland building
    The Docklands building in Hamburg, Germany is shaped like a parallelogram. If a grid were covered the side of the building, the vertices are (0, 0), (86, 0), (49, 55), and (135, 55). Use a cross product to find the area of the side of the building.
  24. Mixed Review
  25. (11-02) Find the angle between ⟨3, 4, 0⟩ and ⟨−2, 0, 1⟩.
  26. (11-02) Evaluate ⟨3, 4, 0⟩ − ⟨−2, 0, 1⟩.
  27. (11-01) Find the distance between (3, 4, 0) and (−2, 0, 1).
  28. (10-08) What is the probability of rolling two dice and having both results be 4 or less?

Answers

  1. ⟨−3, 4, −1⟩
  2. ⟨6, −8, 2⟩
  3. ⟨0, 0, 0⟩
  4. ⟨7, 8, 11⟩
  5. 0
  6. ⟨0, −6, −3⟩
  7. ⟨2, 23 ,−9⟩
  8. \(\left\langle -\frac{\sqrt{30}}{30}, -\frac{\sqrt{30}}{6}, -\frac{\sqrt{30}}{15} \right\rangle\)
  9. \(\left\langle \frac{\sqrt{2}}{2},0,\frac{\sqrt{2}}{2} \right\rangle\)
  10. \(\left\langle -\frac{3\sqrt{115}}{115},\frac{\sqrt{115}}{23},\frac{9\sqrt{115}}{115} \right\rangle\)
  11. 27
  12. 48
  13. −19
  14. −16
  15. 204
  16. 4730 m2
  17. 122.46°
  18. ⟨5, 4, −1⟩
  19. \(\sqrt{42}\)
  20. \(\frac{4}{9}\)