Lab 5: Magnetic Forces and Ampere's Law

---

Abstract

Within this lab, we tested the laws of electromotive forces caused by a change in magnetic flux, as well as the determined the value of e/m of an electron by measuring the radius of curvature through an electric field. In our first part, where we measured an emf within a loop of wire moving into and out of a magnetic field, our results matched fairly well with our expectations. However, we experienced major deviations from the expected values in the second half of the experiment. Possible sources of error could be the difficulty to measure a radius of curvature of a beam of electrons through the refraction of a spherical tube and the loss of energy of the electrons due to collisions with the gases within the tube.

---

Contents

• Abstract
• Objectives
• Methods
• Setup
• Data and Analysis
• Conclusion
• Signature

---

Objectives

• To measure the motional emf induced on a coil passing through a magnetic field.
• To measure the value of e/m by measuring the radius of curvature of an electron beam.

---

Methods

Part 1: Electromotive Force

We connected both the wire coil and the motion sensor to the Pasco interface. We then placed the motion sensor at one end of the track and connected the coil to our cart. We set the magnet next to the track so that the planes of the large magnets were parallel to the plane of the track, and so that the open end faced the track. Giving the cart an initial velocity towards the motion detector, we pushed it so that the attached wire coil passed directly between the magnetic plates. Using Data Studio, we recorded the voltage in the coil as well as the velocity of the cart as the coil passed through the magnetic field of the magnet. We then calculated V_max, recording mean and standard deviation values, and calculated %Error. We also calculated the value V_max/(velocity at V_max) and calculated %Error using the theoretical value NBl. We repeated this procedure four times, using a different initial velocity each time.

Using our V_max and v values from our five runs, we constructed a graph of voltage vs. velocity and fit the data linearly. We used the slope, length of the wire, and number of turns to calculate the strength of the magnetic field B.

Part 2: Straight Wire

With the Helmholtz coils powered on, we varied the voltage to produce five different currents. We then measured the radius of curvature for the electron beam produced by each current.

We brought a large magnet near the tube and observed the effects upon the beam.

We recorded the voltage of the filament heater and the voltage of the electron accelerator. We also recorded the radius of the Helmholtz coils and the number of turns of wire in the coils.

Using the following equation, we calculated the five values for B.

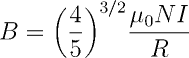
We then used our data to produce a linear plot where the slope of the line of best fit would be equal to 2V/B^2*R^2, which produced our e/m value, and then compared that value to the theoretical value.

---

Setup

Materials:

• Motion sensor
• Pasco 1.2m dynamics track
• Permanent magnet
• Banana clips
• Bell Gauss meters with Hall element probes
• Science Workshop and Graphical Analysis software
• e/m apparatus

Our setup for part 1

Our setup for part 2

Closeup for our setup for part 2

---

Data and Analysis

Part 1 - Electromotive Force

Graph for the trial run #1

μ and σ for trial run #1

μ and σ for maximum voltage in first trial run #1

Graph for the trial run #2

μ and σ for trial run #2

μ and σ for maximum voltage in first trial run #2

Graph for the trial run #3

μ and σ for trial run #3

μ and σ for maximum voltage in first trial run #3

Graph for the trial run #4

μ and σ for trial run #4

μ and σ for maximum voltage in first trial run #4

Graph for the trial run #5

μ and σ for trial run #5

μ and σ for maximum voltage in first trial run #5

Graph plotting average velocity vs. average maximum voltage

Measured strength of magnet=0.1733T
Inner width of coil=0.052m
Outer width of coil=0.068m
Average width of coil=0.060m

Velocity(m/s)	Voltage(V)	Standard Deviation for Voltage(V)	Percent Error
0.46	0.478	0.004	0.84%
0.15	0.143	0.013	9.09%
0.24	0.229	0.011	4.80%
0.33	0.321	0.012	3.74%
0.45	0.445	0.009	2.02%

V_max/v=1.05485Tm
NBl=1.0398
%Error=1.45%

V_max=NBlv
B=(V_max/v)/(Nl)
B_experimental=0.1758T
B_measured=0.1733T
%Error=1.45%

The percent error calculated individually for each voltage is probably due to our fairly crude set up. From past experience with the Pasco carts and tracks, we know that they tend to produce less-than-smooth curves for velocity. This becomes especially apparent as velocity decreases. We found lower velocities to be correlated with higher percent errors. A probable explanation for this correlation is that lower velocities will produce lower voltages, which will be more likely to be swallowed up by sensor noise and the imperfect motion of the cart. This interferences ultimately result in less-correlated mean values for voltage.

However, our calculated error for the magnetic field tended to be much lower than the error for the individual voltages. This is because the percent error for voltage and the percent error for magnetic field are not measuring the same things. The percent error for the magnetic field is measuring the agreement of the the mean values for the individual voltages. The percent error for the individual voltages is the agreement of the points used to calculate said voltages. So it is reasonable to have a lower percent error for the magnetic field than for the individual voltages.

Part 2 - e/m Experiment

Filament heater = 5V
Accelerator voltage = 243V
Permeability of free space = 1.257E-6Tm/A
N of Helmholtz coil = 130 turns
Radius of Helmholtz coil = 0.145m

Accepted e/m
= 1.6021766E-19C/9.10938E-31kg
= 1.75882E11C/kg

Diameter(m)	Radius(m)	Voltage(V)	Current(A)	Experimental Field(T)	X(r^2)(m^2)	Y (2V/B^2)(Cm^2/kg)	e/m(C/kg)
0.089	0.0445	8.0	1.07	8.628E-04	1.980E-03	6.528E+08	3.297E+11
0.085	0.0425	8.2	1.03	8.306E-04	1.806E-03	7.045E+08	3.900E+11
0.084	0.0420	8.4	1.06	8.548E-04	1.764E-03	6.652E+08	3.771E+11
0.086	0.0430	8.8	1.12	9.032E-04	1.849E-03	5.958E+08	3.222E+11
0.084	0.0420	9.0	1.17	9.435E-04	1.764E-03	5.460E+08	3.095E+11

2V/B² vs. r² The slope of these lines should be the ratio e/m

m_mx+b=1.316E11
m_Ax=3.449E11
m_theoretical=1.758E11
%Error_mx+b=25.1%
%Error_Ax=96.2%

When we moved an external magnet closer to the electron beam, we noticed that its path was warped. Depending on the orientation of the magnet, we could force the beam into the side of the tube, change the radius of the circle, or even make the beam spiral back in a helix until it collided with the back side of the tube

The catastrophic deviation in our value of e/m can be attributed to the less than ideal conditions that we were using in the lab. The electrons were moving in a circle through a spherical tube, making it very difficult to measure the radius of the circle, as the refraction due to the curved glass surface made it difficult to estimate the correct radius. The electrons may also have been slowing down considerably as they moved through the gas, losing much of their initial energy through collisions.

We fitted two lines to our data. Neither was terribly close to the accepted e/m value. We expected the proportional fit to be much closer to the accepted value than the mx+b fit, but it turned out to be a full 96% off.

---

Conclusion

The first part of this lab was a success. Our experimental results and calculations correlated very well to the field that we measured with the teslameter. In the second half of the lab, we experienced greater problems finding experimentally the ratio of e/m for an electron.

In the first part of the experiment, our error was fairly insignificant. Most of the error can be attributed to friction of the cart and the track, and any tension that the wires that were attached to the cart caused as it moved along. More thorough and rigorous analysis could be performed to compensate for these factors, but the results as they stand confirm the equations used fairly well.

In the second part of the experiment, we barely claim that our ratio was in the right magnitude of 10. Neither of the lines we used to find the ratio were close to accurate. Our greatest difficulty was finding the exact radius of the beam of electrons. We had to rely on human observation to record minute changes in distances. Also, the beam of electrons was not perfectly circular, as they were losing energy to the gas along the path. This would make the radius of curvature misleadingly large.

Overall, I believe that the first part of the lab stands well as it is. If the cart itself were a bit heavier, it would be more resistant to any changes in velocity through friction and tension of the wires. As for the second part, a lower energies for the electron beam would make the radius wider, and easier to measure. This would require a much larger setup, however, and more expensive equipment. Perhaps photo analysis and a compensation for Snell's law would reveal the e/m ratio more accurately.

---

Signature